General

Highest value prep document is probably Shivi’s Final Slides.

Countability

Remember to show that the function is TOTALLY-DEFINED and WELL-DEFINED for the proof to be valid!

Countable: Use different sets

To prove $A$ is countable we can also show an injection from $A\to C$ where $C$ is any countable set:

• union
• direct product
• finite bitstring of a countable set, as these are all countable.

Countable: Injection delimiter

We can use a character like $\sim$ or # which is not in $\mathbb{N}$ to use as a delimiter when concatenating. This resolves issues like "$12||1$" and "$1||21$" mapping to the same natural number when concatenated in a function $f:A\to (\{\sim \}\cup \mathbb{N}{)}^{\ast }$.

Countable: Prefix to fix leading 0s

We can add a $1||...$ to the start of our injection’s output to prevent leading $0$s from being an issue.

Uncountable: By injection from $\{0,1{\}}^{\infty }$

See exercise Sheet 6.6.3.

We define an injection $g$ from the uncountable set $\{0,1{\}}^{\infty }$ to $S$. Let $g:\{0,1{\}}^{\infty }\to S$, $\alpha \to f$ where $f(k)=\{\begin{array}{ll}0& \text{if }k{\equiv }_{2}1\\ {\alpha }_{k/2}& \text{if }k{\equiv }_{2}0\end{array}$ $\text{Im}(g)\subseteq S$ as:

• $\forall f\in \text{Im}(g)$, $\forall i\in \mathbb{N}$ $f(i)=0$ or $f(i+1)=0$
• $\forall f\in \text{Im}(g)$, $\forall i\in \mathbb{N}$ $f(i)\le 1$ it is thus clear that the image is thus a subset of $S$ as the conditions of $S$ are satisfied.

$g$ is injective as for $\alpha$ and $\beta$ in $S$ distinct, let $k$ be the first position at which they differ. Then ${\alpha }_k\ne {\beta }_k$. Let $h(\alpha )=f_{\alpha }$ and $h(\beta )=f_{\beta }$. By construction, $f_{\alpha }(2\cdot k)={\alpha }_k\ne {\beta }_k=f_{\beta }(2\cdot k)$ thus $f_{\alpha }\ne f_{\beta }$ and thus $g$ injective.

At the end show that if it was countable, we’d have a contradiction with $\{0,1{\}}^{\infty }\prec \mathbb{N}$. Thus it’s uncountable.

Uncountable: By Diagonalisation

See exercise Sheet 6.6.1.

Sets, Relations and Partial Orders

Lattices

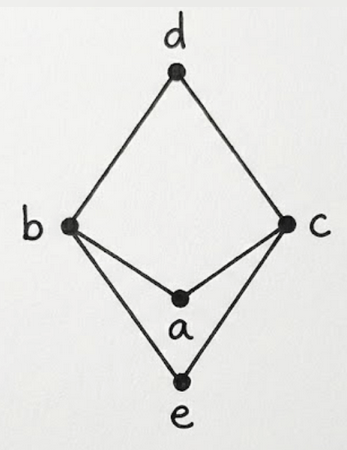is not a lattice, as $\{b,c\}$ do not have a unique greatest lower bound, as both $a$ and $e$ lower bound them, but are not comparable themselves, i.e. there’s no least/greatest.

Number Theory

Ideals, etc…

When assuming there is a minimum positive element in a subset of $\mathbb{N}$, then we have to show that a positive element exists.

Modulo Exercises

Modular reduction $R_a(b^c)$

We can reduce $c$ by $\phi (a)$ if $\gcd (a,b)=1$, i.e. $a$ and $b$ are coprime.

Errors:

• Note that we can’t simply reduce by $a$.
• Give the answer as a positive number, i.e. wrap around the modulo. $R_6(7)\ne -5$ as the $R$ remainder function is defined for positive remaineders.

Case Distinction

Try a table if the mod is not too large. Ex: $a,b\in \mathbb{Z}{a}^2=b^2{\equiv }_{7}0⟹a^2{\equiv }_{7}0\wedge b^2{\equiv }_7=0$?

We can argue $\mathrm{mod}3$ here. Since $p$ is prime, $p{\equiv }_{3}1\text{ or }2$ and not $0$. $f(1){\equiv }_{3}0$ and $f(2){\equiv }_3=0$ thus all $f(p)$ are divisible by 3 and therefore not prime.

Formal Answer from Exams: First see that for $p=2,3$ is composite:

• $f(2)=2^4+2^2+1=16+4+1=21=3\cdot 7$
• $f(3)=3^4+3^2+1=81+9+1=91=7\cdot 13$ Now we consider all primes $p>3$ modulo $3$: either $R_3(p)=1⟹R_3(f(p))=R_3(1^4+1^2+1)=0$ and thus it is divisible by $3$ and thus not prime or $R_3(p)=2⟹R_3(f(p))$ $=R_3(2^4+2^2+1)=R_3(16+4+1)=R_3(21)=0$ and thus it is divisible by $3$ and thus not prime. The case $R_3(p)=0$ for $p>3$ does not occur as else $p$ would be divisible by $3$ and thus not prime. We conclude that $f(p)$ is not prime for $p$ prime.

GCD of two absurd numbers

We can reduce a number in a gcd modulo the second number by Lemma 4.2 ($\gcd (a,b)=\gcd (a,R_a(b))$).

Example: Compute the $\gcd (81,48+3^{25})$.

1. We can use the fact that $81=3^4$ and reduce $3^{25}{\equiv }_{3^4}0$. Then by Lemma 4.2 $\gcd (81,48+3^{25})=\gcd (81,48)=3$.
2. We can also factor everything into primes, using $81=3^4$ and $48=3\cdot 2^4$ thus $48+3^{25}=3\cdot (2^4+3^{24})$. The rest $2^4+3^{24}$ is not divisible by $3$ anymore since $2^4+3^{24}{\equiv }_3=2^4=2$.

GCD Possible Values

Don’t forget to give $1$ as a possible solution.

Set of Solutions to a congruence system

We can use normal techniques to solve the system of equations. Remember to give the solutions in the required form at the end: $(x,y)\in {\mathbb{Z}}_{11}\times {\mathbb{Z}}_{11}$, ex: $(10,1)$.

If the two equations are colinear, we just have to solve one of them (state that they are colinear though) Example.

CRT Solving

TODO: Exact steps

A CRT system has a unique solution $\mathrm{mod}M$ if and only if the $m_1,m_2,\dots ,m_i$ all are coprime.

If that is not the case, we have to check if we can decompose equations into smaller ones: \begin{align*} x \equiv_{10} 3 \\ x \equiv_{2} 1 \\ x \equiv_3 2 \end{align*} has a solution even though $10$ and $2$ are coprime as we can decompose $x{\equiv }_{10}3$  into $x{\equiv }_{5}3$ and $x{\equiv }_{2}3{\equiv }_{2}1$ which matches the other equation. Thus the solution is still unique.

Algebra Exercises

Prove Subgroup

We need to show: 0. (Subset)

1. Closure
2. Neutral element
3. Inverses are in Subgroup

Number of Subgroups of $⟨{\mathbb{Z}}_a\times {\mathbb{Z}}_b⟩$

The formula here is ${\sum }_{a|m\wedge b|n}\gcd (a,b)$.

For $⟨{\mathbb{Z}}_2\times {\mathbb{Z}}_6⟩$ this gives $a\in \{1,2\}$ and $b\in \{1,2,3,6\}$ which leads to the following: ${\sum }_{b|6}\gcd (1,b)=1+1+1+1=4$ and ${\sum }_{b|6}\gcd (2,b)=1+2+1+2=6$ which gives $4+6=10$. Answer

Number of Subgroups of ${\mathbb{Z}}_n^{\ast }$

Isomorphic to ${\mathbb{Z}}_{\phi (n)}$, and that group has ${\prod }_i(e_i+1)$ divisors → thus subgroups.

Order of element in direct product

$G$ group and $x\in G$ s.t. $\text{ord}(x)=8$. What is the order of $(x^{10},x^{12})\in G\times G$?

We have $\text{lcm}(10,8)=40$ and $40=10\cdot 4$, thus $\text{ord}(x^{10})=4$. In the same way $\text{ord}(x^{12})=2$.

Therefore $\text{ord}((x^{10},x^{12}))=\text{lcm}(2,4)=4$. Indeed $(x^{10},x^{12}{)}^4=(x^{40},x^{48})=((x^8{)}^5,(x^8{)}^6)=((1,1))$. https://exams.vis.ethz.ch/exams/j3t8gtp0.pdf?answer=it57ztn6rqzypeaa

Maximum order of direct product

$\text{lcm}(n,m)$ for ${\mathbb{Z}}_n\times {\mathbb{Z}}_m$ see.

Generators of ${\mathbb{Z}}_m^{\ast }$

To find a generator of ${\mathbb{Z}}_{14}^{\ast }$, we list all elements first $=\{1,3,5,9,11,13\}$ Note that the order is $6$. As the subgroup order divides the group order, all subgroups have order $1,2,3,6$. Therefore we need to find an element such that $ord(x)=6$ and $ord(x)\ne 1,2,3$.

Inverses in a ${\mathbb{Z}}_n[x{]}_{x^2+1}^{\ast }$ (group)

The neutral element in such a group is $1$ (it’s multiplicative). Inverse of $a(x)$: $a(x)b(x){\equiv }_{x^2+1}1⟹a(x)b(x)=1+k\cdot (x^2+1)$.

Example Inverse of $x+2$ in ${\mathbb{Z}}_7[x{]}_{x^2+2}^{\ast }$ We want to solve $(x+2)(ax+b){\equiv }_{7}1$ ($ax+b$ as there’s no degree $2$ polynomials in this group). $(x+2)(ax+b)=a{x}^2+bx+2ax+2b=a{x}^2+(2a+b)x+2b$. We have $x^2{\equiv }_{x^2+2}-2{\equiv }_{7}5$ in this group (calculate $x^2{\equiv }_{x^2+1}$ to simplify here), thus $(2a+b)x+2b+5a{\equiv }_{x^2+1}1$ is our final equation. We solve these two component equations:

• $2a+b{\equiv }_{7}0$ (we want $0x$)
• $2b+5a{\equiv }_{7}1$ (for the $1$ at the end)

$b=-2a=5a$ and $2\cdot (5a)+5a{\equiv }_{7}a{\equiv }_{7}1$ thus $a=1$ (if it’s not clear here, for example $5a{\equiv }_{7}1$, we take the modular inverse of $5\mathrm{mod}7$) $2a+b{\equiv }_{7}2+b{\equiv }_{7}0$ thus $b=5$.

Find zero-divisors of ${\mathbb{Z}}_{25}$

Note that this only makes sense in ${\mathbb{Z}}_n$ without $\ast$ otherwise there wouldn’t be any! We have to list all multiples of the divisors of $n$, so in the case of $25=5^2$ its divisors are $1,5,5$ thus the multiples are $5,10,15,20$.

$0$ not in the multiplicative group

Because $0$ has no inverse, for any multiplicative group $0\notin {\mathbb{Z}}_n^{\ast }$, etc… $\gcd (0,n)=n$!

Generators of Subgroups of ${\mathbb{Z}}_3\times {\mathbb{Z}}_4$

Isomorphic to ${\mathbb{Z}}_{12}$ which has $(1+1)\cdot (2+1)=6$ subgroups. The groups are $\{0\},\{0,6\},\{0,4,8\},\{0,3,6,9\},\{0,2,4,6,8,10\},{\mathbb{Z}}_{12}$. Note that they are generated respectively by $0,6,4,3,2,1$ We use the canonical isomorphism $(R_3(a),R_3(b))$ to get the generators of ${\mathbb{Z}}_3\times {\mathbb{Z}}_4$ subgroups.

• $(0,0)$
• $(R_3(6),R_4(6))=(0,2)$
• $(R_3(4),R_4(4))=(1,0)$
• $(R_3(3),R_4(3))=(0,1)$
• $(R_3(2),R_4(2))=(2,2)$
• $(R_3(1),R_4(1))=(1,1)$ Which are all the generators.

Find all which aren’t units

In ${\mathbb{Z}}_7[x{]}_{x^2-1}$ we have $x^2-1=(x+1)(x-1)$ thus all that don’t have a factor are units. Thus non-units are $(x+1)$, $(x+6)$ and all multiples: $2(x+1),3(x+1),4(x+1),5(x+1),6(x+1)$ and $2(x-1),\dots$

Disprove Isomorphism

Disprove that ${\mathbb{Z}}_{12}^{\ast }$ and ${\mathbb{Z}}_4$ are isomorphic. ${\mathbb{Z}}_{12}^{\ast }$ has $4$ elements but is not cyclic! ${\mathbb{Z}}_4$ is cyclic, thus there cannot be an isomorphism.

Logic Exercises

Find CNF and DNF formulas

Note that CNF and DNF are not mutually eclusive.

Circle all such that $F\models G$

Watch out for tautologies as $F\models \top$ is always true! $F=\forall xP(x)$ models $G=(Q(y)\to Q(z))\vee (Q(z)\to Q(y))$ even though they share nothing as $G$ is a tautology.

Resolution Calculus Proofs

The statement $\{F_1,\dots ,F_n\}\models G$ is equivalent to $\{F_1,\dots ,F_n,\neg G\}$ is unsatisfiable (Lemma 6.3). … Using the resolution calculus we have shown that $\{F_1,\dots ,F_n,\neg G\}{⊢}_{Res}\varnothing$ thus $\{F_1,\dots ,F_n,\neg G\}$ is unsatisfiable. Therefore, $\{F_1,\dots ,F_n\}\models G$ (Lemma 6.3).

Proof Systems

Prove that: ”${\Pi }_3$ complete $⟹$ ${\Pi }_1\vee {\Pi }_2$ complete

We use an indirect proof. Assume that ${\Pi }_1\wedge {\Pi }_2$ are incomplete. Then there exist ${\tau }_1(s_1)=1$ and ${\tau }_2(s_2)=1$ (otherwise vacuously complete). Thus $\forall (p_1,p_2)\in P_1\times P_2$ we have ${\varphi }_1(s_1,p_1)=0$ and ${\varphi }_2(s_2,p_2)=0$. Thus ${\tau }_3(s_1,s_2)=1$ but forall $(p_1,p_2)$\phi_3((s_1, s_2),(p_1, p_2)) = 0$.Thus$\Pi_3$ incomplete.

Semantics Proofs

We can transform:

• ${\mathcal{A}}_{[x\to u]}(F)=1$ for all $u\in U^{\mathcal{A}}$ into ${\mathcal{A}}_{[x\to u]}(F)\ne 0$ for all $u\in U^{\mathcal{A}}$ (according to Leo)

General Formula

Let $\mathcal{A}$ be a suitable interpretation for both $...$ (LHS) and $...$ (RHS) such that it is a model for $...$ (LHS).

$\mathcal{A}\models F⟹\mathcal{A}(F)=1\text{ (def. of a model)}$ Perform the changes here until we get $\mathcal{A}(G)=1⟹\mathcal{A}\models G\text{ (def. of a model)}$Thus the statement holds and $F\models G$.

Note that the transformations that one is allowed to do generally follow those that are noted in Lemma 6.7. They can’t be justified in natural language, as they just make sense (by Leo in Discmath Chat).

Note that if we are asked to prove a literal statement from Lemma 6.7, we obviously can’t just use it directly. Like here in the exercise sheet for $\exists x\exists yF\equiv \exists y\exists xF$:

The following step (swap) had to be justified: \begin{align} \iff & \mathcal{A}_{[x \to u][y \to v]}(F) = 1 \text{ for some } u \in U^{\mathcal{A}} \text{ and some } v \in U^{\mathcal{A}} \tag{3} \\ \iff & \mathcal{A}_{[y \to v][x \to u]}(F) = 1 \text{ for some } v \in U^{\mathcal{A}} \text{ and some } u \in U^{\mathcal{A}} \tag{4} \end{align} was justified using

• ${\xi }^{{\mathcal{A}}_{[x\to u][y\to v]}}(x)=u={\xi }^{{\mathcal{A}}_{[y\to v][x\to u]}}(x)$,
• ${\xi }^{{\mathcal{A}}_{[x\to u][y\to v]}}(y)=v={\xi }^{{\mathcal{A}}_{[y\to v][x\to u]}}(y)$,
• and on all other variable symbols $x_i$ we have ${\xi }^{{\mathcal{A}}_{[x\to u][y\to v]}}(x_i)$ $={\xi }^{\mathcal{A}}(x_i)={\xi }^{{\mathcal{A}}_{[y\to v][x\to u]}}(x_i)$.

Semantics of quantifiers

When substituting a bound variable after applying the semantics, of a quantifier, we don’t swap the variable for the bound one: $A_{[x\to u]}(Q(x))$ and not $A_{[x\to u]}(Q(u))$!

Prenex form

Prenex parentheses

Remember that quantifiers bind harder than operators!! Thus for the prenex form we need parentheses all around.

Proper syntax of substitution by function

See ansWwer.

Example: $\forall zP(z)\models \forall zP(f(z))$. As $\mathcal{A}$ is suitable for both sides, $\mathcal{A}$ defines a function $\mathcal{A}(f)$, denoted $f^{\mathcal{A}}$.

Then we can say \begin{align*} A_{[z \rightarrow u]}(P(z)) = 1 && \text{ for all } u \in U^{\mathcal{A}} \\ \mathcal{A}_{[z \rightarrow f^\mathcal{A}(u)]}(P(z)) = 1 && \text{ for all } u \in U^\mathcal{A} \\ \mathcal{A}_{[z \rightarrow u]}(P(f(z))) = 1 && \text{ for all } u \in U^\mathcal{A} \end{align*} Justifications:

1. $f^{\mathcal{A}}(u)\in U^{\mathcal{A}}$ for $u\in U^{\mathcal{A}}$. And as ${\mathcal{A}}_{[z\to u]}(P(z))=1$ for all $u\in U^{\mathcal{A}}$, this doesn’t change anything.
2. ${\mathcal{A}}_{[z\to f^{\mathcal{A}}(u)]}(z)={\mathcal{A}}_{[z\to u]}(f(z))$ means we can simply replace $z$ by $f(z)$.

Proper syntax of free → bound by $\exists$

See answer.

We can quantify a free variable with an existential quantifier $\exists$ using the following justification.

• $\mathcal{A}(x)⟹$ ${\mathcal{A}}_{[x\to x^{\mathcal{A}}]}(P(x))=1$ as $\mathcal{A}={\mathcal{A}}_{[x\to x^{\mathcal{A}}]}$ (this is the definition of interpretation).
• ${\mathcal{A}}_{[x\to x^{\mathcal{A}}]}(P(x))=1⟹$ ${\mathcal{A}}_{[y\to x^{\mathcal{A}}]}(P(y))=1$ as $P(x)[x/y]=P(y)$ (substitution)
• ${\mathcal{A}}_{[y\to u]}(P(y))=1$ for some $u\in U^{\mathcal{A}}$ (as $x^{\mathcal{A}}\in U^{\mathcal{A}}$).
• ${\mathcal{A}}_{[y\to u]}(P(y))=1⟹$ $\mathcal{A}(\exists yP(y))=1$ (semantics of $\exists$)

Universal Instantiation

See FS19

When a universal quantifier disappears on the right side of the formula, we use the rule for universal instantiation which states: $\forall xF\models F[x/z]$ We can then just remove the forall and replace the variable by another.

Interpretation for $F$ or $G$ formulas

If we need to find an interpretation for a formula that looks like this $\forall xF$ or $G$, then we need to find a formula that replaces $F$ or $G$! This is written as $F=P(x,y)$ or $G=P(x)\wedge Q(y)$ and not as $F^{\mathcal{A}}=...$ or $F(x)=\mathrm{1...}$!