Chapter 5

Algebra

5.1 Arity of a function

An operation on a set $S$ is a function $S^n\to S$, where $n\ge 0$ is called the arity of the operation.

We have unary and binary operations. A nullary operation is called a constant.

5.2 Algebra

An algebra (or algebraic structure or $\Omega$-algebra) is a pair $⟨S;\Omega ⟩$ where $S$ is the set (the carrier of the algebra) and $\Omega =({\omega }_1,\dots ,{\omega }_n)$ is a list of operations on $S$.

Example $⟨\mathbb{Z};+,-,0,\cdot ,1⟩$ denotes the integers with the two binary operations $+$ and $\cdot$ and the unary operation $-$ (taking the negative) and two constants $0$ and $1$, the neutral elements of addition and multiplication.

You can draw a sort of table that represents the function on an algebra:

*	a	b	c
a	b	c	a
b	c	a	b
c	a	b	c
From this we can read of certain properties.

Monoids

An algebra can have special properties, for example: (1) a neutral element, (2) associativity and (3) inverse elements. Commutativity is not as interesting.

5.3 Neutral Elements

A left [right] neutral element (or identity relation) of an algebra $⟨S;\ast ⟩$ is an element $e\in S$ such that $e\ast a=a$ ($a\ast e=a$ ) for all $a\in S$. If $e\ast a=a\ast e=a$ for all $a\in S$, then $e$ is simply called neutral element.

If the operation is addition, then $e$ is usually denoted $0$, if the operation is multiplication then the operation is denoted $1$.

5.1 Uniqueness of neutral element

If $⟨S;\ast ⟩$ has both a left and a right neutral element, then they are equal. In particular $⟨S;\ast ⟩$ can have at most one neutral element.

Commutativity and unique neutral element

The uniqueness of the neutral element does not imply that the group is abelian.

Think of the identity matrix $I_3$ for the group of matrices $\in {\mathbb{R}}^3$ and element-wise multiplication. $A\cdot I_3=I_3\cdot A$ even though multiplication is not commutative.

Example The empty sequence $ϵ$ is the neutral element of the group of sequences over the alphabet with concatenation.

5.4 Associativity

A binary operation $\ast$ on a set $S$ is associative if $a\ast (b\ast c)=(a\ast b)\ast c$ for all $a,b,c\in S$.

Associativity is very important! It means that $a_1\ast a_2\ast \cdots \ast a_n$ is uniquely defined and independent of the order of “execution”: $(((a\ast b)\ast c)\ast d)=((a\ast b)\ast (c\ast d))=(a\ast ((b\ast c)\ast d))$

Example Not all operations are associative, exponentiation on the integers is not for example.

5.5 Monoids

A monoid is an algebra $⟨M;\ast ,e⟩$ where $\ast$ is associative and $e$ is the neutral element.

Example $⟨\mathbb{Z};+,0⟩$, $⟨{\mathbb{Z}}_m;\oplus ,0⟩$ are examples of monoids.

Groups

5.6 Inverses

A left [right] inverse element of an element $a$ in an algebra $⟨S;\ast ,e⟩$ with neutral element $e$ is an element $b\in S$ such that $b\ast a=e$ ($a\ast b=e$). If $b\ast a=a\ast b=e$, then $b$ is simply called an inverse of $a$.

5.2 Uniqueness of the inverse

In a monoid $⟨M;\ast ,e⟩$, if $a\in M$ has a left and right inverse, then they are equal. In particular, $a$ has at most one inverse.

Example A function $f\in A^A$ has a left inverse if $f$ is injective, it has a right inverse if $f$ surjective. Hence $f$ has an inverse $f^{-1}$ if and only if $f$ is bijective.

5.7 Group

A group is an algebra $⟨G;\ast ,\hat{},e⟩$ satisfying the following axioms:

• G1 $\ast$ is associative
• G2 $e$ is a neutral element: $a\ast e=e\ast a=a$ for all $a\in G$.
• G3 Every $a\in G$ has an inverse element $\hat{a}$, i.e. $a\ast \hat{a}=\hat{a}\ast a=e$.

*We can write $⟨G;\ast ⟩$ instead of the longer version. The inverse in a group with addition is denoted $-a$ and the inverse in a group with multiplication is $a^{-1}$.

If we refer back to the tables representing the results of the operation, we can see that there never can be two elements leading to the same element under the operation. Thus every row and column has to contain every element once (inverse needs to exist).

Proving something is a group

We need to prove G1, G2, G3. We only need to prove closure if it’s not obvious that the operation’s range $Im(+)$ for example is identical to the group’s carrier.

5.8 Abelian or Commutative Groups

A group $⟨G;\ast ⟩$ (or monoid) is called commutative or abelian if $a\ast b=b\ast a$ for all $a,b\in G$.

5.3 Group properties

For a group $⟨G;\ast ,\hat{},e⟩$ we have for all $a,b,c\in G$:

• (i) $\widehat{(\hat{a})}=a$.
• (ii) $\widehat{a\ast b}=\hat{b}\ast \hat{a}$.
• (iii) Left cancellation law: $a\ast b=a\ast c⟹b=c$.
• (iv) Right cancellation law: $b\ast a=c\ast a⟹b=c$.
• (v) The equation $a\ast x=b$ has a unique solution $x$ for any $a$ and $b$. So does the equation $x\ast a=b$.

Useful properties of groups

• $a=b\iff ca=cb$ (as you can cancel out the $c$ by the cancellation laws)
• $a=b\iff ac=bc$ (same…)

We want the axioms of a theory to be minimal. We can show that $\{G_1\wedge G_2^{\prime }\wedge G_3^{\prime }\}\models G_2(G_3)$. We only need to have $a\ast e=a$ for G2, which we call axiom G2’. The equation $e * a = a* is then implied by all axioms. The same can be done for G3, thus creating G3’.

Examples The set $S_n$ is the set of $n!$ permutations of $n$ elements (the set of bijections $\{1,\dots ,n\}\to \{1,\dots ,n\}$). A bijection has an inverse $f^{-1}$. It follows from the associativity of function composition that the composition of these permutations is also associative. We thus have $⟨S_n;\circ ,{}^{-1},\text{id}⟩$ the symmetric group on $n$ elements. $S_n$ is non-abelian for $n\ge 3$.

Reflections and symmetries of geometric figures are another important sources of groups (ex: 8 symmetries on the cube).

Direct Products

5.9 Direct Product

The direct product of $n$ groups $⟨G_1;{\ast }_1⟩,\dots ,⟨G_n;{\ast }_n⟩$ is the algebra $⟨G_1\times \cdots \times G_n;\star ⟩$ where the operation $\star$ is component-wise: $(a_1,\dots ,a_n)\star (b_1,\dots ,b_n)=(a_1{\ast }_1{b}_1,\dots ,a_n{\ast }_n{b}_n)$

Example The group $⟨{\mathbb{Z}}_5;\oplus ⟩\times ⟨{\mathbb{Z}}_7;\oplus ⟩$. The carrier is ${\mathbb{Z}}_5\times {\mathbb{Z}}_7$ with the neutral element $(0,0)$. It follows from the CRT that $⟨{\mathbb{Z}}_5;\oplus ⟩\times ⟨{\mathbb{Z}}_7;\oplus ⟩$ is isomorphic to $⟨{\mathbb{Z}}_{35};\oplus ⟩$.

Homomorphisms

5.10 Group Homomorphism

For two groups $⟨G;\ast ,\hat{},e⟩$ and $⟨H;\star ,\stackrel{~}{},e^{\prime }⟩$, a function $\psi :G\to H$ is called a group homomorphism if, for all $a$ and $b$, $\psi (a\ast b)=\psi (a)\star \psi (b)$

If $\psi$ is a bijection from $G$ to $H$, then it is called an isomorphism, and we say that $G$ and $H$ are isomorphic and write $G\simeq H$.

What this means is that it does not matter if we first apply the function and then perform the operation or if we perform the operation and then map the result. The same arguments produce the same output in both groups.

Does Every Homomorphism have to be injective? No, we could map all elements to the neutral element, which would still satisfy the property.

This picture clarifies the properties of homomorphisms:

• $h:G\to H$ is a homomorphism here.
• $\ker h$ is the kernal of the map $h$, which is basically the nullspace (set of all elements mapped to the neutral).
• $\text{im}h$ is the image, the set of all elements mapped to $H$.
• $aN$ is the coset where $N=\ker h$, thus $aN=\{a{\ast }_{G}g|g\in N\}$.

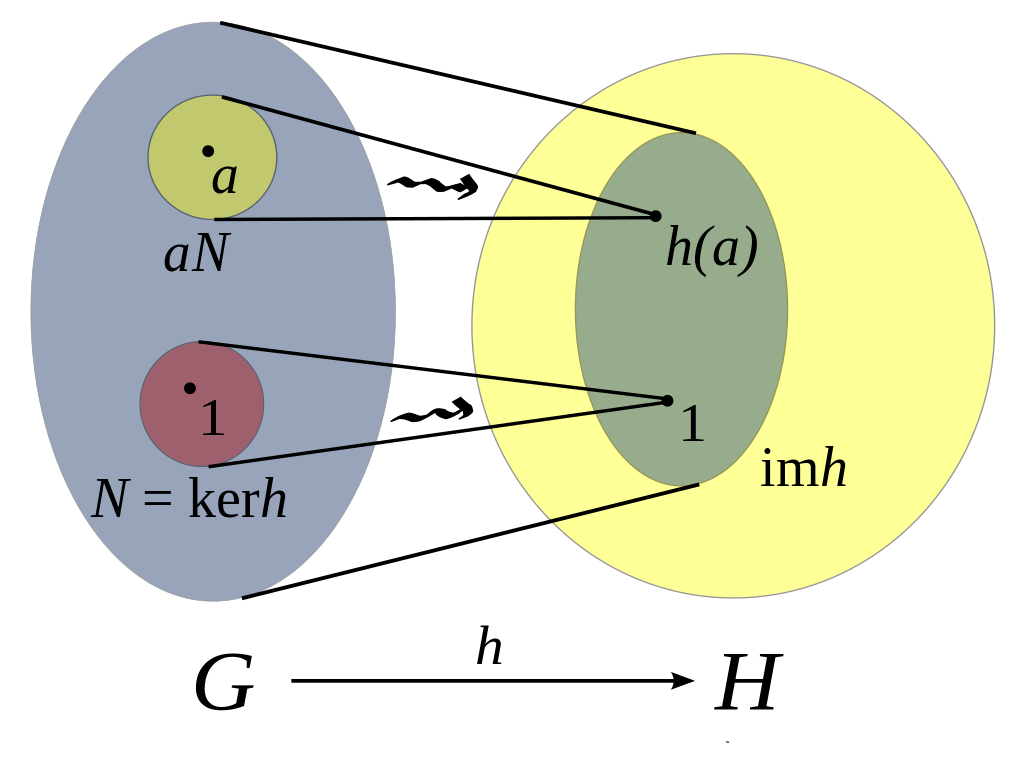
Isomorphisms: An isomorphism is simply a homomorphism which is also bijective. This means that the structure is preserved both ways, i.e. the groups behave the same. Think of two jigsaw puzzles that look completely different, but the same piece goes into the same place on both (same cutout was used).

Prove an Isomorphism:

1. Define a Candidate Map: Identify a function $\varphi :G\to H$ that you suspect to be an isomorphism.
2. Verify the Map is Well-Defined: Ensure that the proposed map is unambiguous and consistent. That is, for any $g\in G$, $\varphi (g)$ is uniquely determined.
3. Verify the Map is Totally Defined: Confirm that the map is defined for all elements of $G$ (i.e., $\varphi$ applies to every element of $G$).
4. Verify the Map Maps to the Codomain: Ensure that $\varphi (g)\in H$ for all $g\in G$ so that the image of $\varphi$ lies entirely within $H$.
5. Check the Homomorphism Property: Verify that $\varphi (g_1\cdot g_2)=\varphi (g_1)\cdot \varphi (g_2)$ for all $g_1,g_2\in G$. This ensures the map preserves the group operation.
6. Check Injectivity: Prove that $\varphi$ is one-to-one by showing that if $\varphi (g_1)=\varphi (g_2)$, then $g_1=g_2$​.
7. Check Surjectivity: Prove that $\varphi$ is onto by demonstrating that for every $h\in H$, there exists $g\in G$ such that $\varphi (g)=h$.
8. Conclude Isomorphism: If the map satisfies the homomorphism property, is well-defined, maps to the codomain, and is bijective, then $\varphi$ is an isomorphism, and $G\simeq H$.

5.5 Group Homomorphism properties

A group homomorphism $\psi$ from $⟨G;\ast ,\hat{},e⟩$ to $⟨H;\star ,\stackrel{~}{},e^{\prime }⟩$ satisfies (not iff. but only $⟹$):

• (i) $\varphi (e)=e^{\prime }$
• (ii) $\varphi (\hat{a})=\widetilde{\varphi (a)}$ for all $a$.

Example The logarithm function is a group homomorphism from $⟨{\mathbb{R}}^{>0};\cdot ⟩$ to $⟨\mathbb{R},+⟩$ since $\log (a\cdot b)=\log a+\log b$. (It’s also an isomorphism) Example The projection of points in ${\mathbb{R}}^3$ down to ${\mathbb{R}}^2$ is a homomorphism but not an isomorphism as it’s not a bijection.

Subgroups

5.11 Subgroups

A subset $H\subseteq G$ of a group $⟨G;\ast ,\hat{},e⟩$ is called a subgroup of $G$ if $⟨H;\ast ,\hat{},e⟩$ is a group, i.e., if $H$ is closed with respect to all operations:

• (1) $a\ast b\in H$ for all $a,b\in H$
• (2) $e\in H$
• (3) $\hat{a}\in H$ for all $a\in H$

Trivial subgroups

For any group $G$ there exist two trivial subgroups:

• the set $\{e\}$
• $G$ itself.

Example The group ${\mathbb{Z}}_{12}$ has the following subgroups $\{0\}$, $\{0,6\}$, $\{0,4,8\}$, $\{0,3,6,9\}$, $\{0,2,4,6,8,10\}$ ${\mathbb{Z}}_{12}$.

Order of a Group Element and Group

Notation

We use the following notation to talk about order:

• $a^0=e$
• $a^n=a\cdot a^{n-1}$ for $n\ge 1$
• $a^n=(a^{-1}{)}^{|n|}$ for $n\le -1$

The following laws therefore also hold:

• $a^m\cdot a^n=a^{m+n}$
• $(a^m{)}^n=a^{mn}$

5.12 Order of an element

Let $G$ be a group and let $a$ be an element of $G$. The order of $a$, denoted $\text{ord}(a)$, is the least $m\ge 1$ such that $a^m=e$, if such an $m$ exists: $\text{ord}(a)=\min \{n\ge 1|a^n=e\}\cup \{\infty \}$

$\text{ord}(a)$ is said to be infinite otherwise, written $\text{ord}(a)=\infty$.

Some useful facts

• By definition, $\text{ord}(e)=1$.
• If $\text{ord}(a)=2$ for some $a$, then $a^{-1}=a$, i.e. $a$ is it’s own self-inverse.
• If $\text{ord}(a)=|G|$, we say $a$ has “volle Ordnung” (such an element must not always exist).

Example The order of $6$ in $⟨{\mathbb{Z}}_{20};\oplus ,\ominus ,0⟩$ is $10$. This can be easily seen since $\text{lcm}(6,20)=10$, i.e. we need to add $6$ to itself $10$ times to reach $60$ which is a multiple of $20$, i.e. $0\text{mod}20$.

Example The order of any integer $a\ne 0$ in $⟨\mathbb{Z};+⟩$ is $\infty$ as we never loop around (carrier $\mathbb{Z}$ is an infinite group)…

5.6 Finite Order in Finite Groups

In a finite group $G$, every element has a finite order.

See proof in script.

5.13 Order of a Group

For a finite group $G$, $|G|$ is called the order of $G$. (same name as the order of an element).

Cyclic Groups

Power modulo order

In a group $G$ of finite order, for $a\in G$ $a^m=a^{R_{\text{ord}(a)}(m)}$ as $a^m=a^{m+\text{ord}(a)}=a^m\cdot a^{\text{ord}(a)}=a^m\cdot e=a^m$.

5.14 Generators

For a group $G$ and $a\in G$, the group generated by $a$, denoted $⟨a⟩$, is defined as $⟨a⟩\stackrel{\text{def}}{=}\{a^n|n\in \mathbb{Z}\}$

This $⟨a⟩$ is a group, the smallest subgroup of a group $G$ containing the element $a\in G$.

For finite groups we have $⟨a⟩=\{e,a,a^2,\dots ,a^{\text{ord}(a)-1}\}$.

Generators of ${\mathbb{Z}}_n$

We know that ${\mathbb{Z}}_n$ is generated by all $a\in {\mathbb{Z}}_n$ for which $\gcd (n,a)=1$.

Proof: Assume ${\mathbb{Z}}_n=⟨a⟩$. This $⟹1\in ⟨a⟩⟹au{\equiv }_{n}1$ And then using Bézout: $⟹au=1+nv⟹au-nv=1⟹\gcd (a,n)=1$

5.15 Cyclic group and generator

A group $G=⟨g⟩$ generated by an element $g\in G$ is called cyclic and $g$ is called a generator of $G$.

• Associativity inherited from $G$
• Neutral element is always in $⟨g⟩$ as $g^0=e$.
• The inverse is $a^n\cdot a^{-n}=e$ by definition.

A group can have more than one generator. In particular, if $⟨g⟩$ is a generator, then $⟨\hat{g}⟩$ is also a generator.

Example $⟨1⟩=\mathbb{Z}$ and $⟨-1⟩=\mathbb{Z}$

5.7 Isomorphism from cyclic groups to additive groups

A cyclic group of order $n$ is isomorphic to $⟨{\mathbb{Z}}_n;\oplus ⟩$ (and hence abelian).

Standard notation for cyclic groups

We use $⟨{\mathbb{Z}}_n;\oplus ⟩$ as our standard notation for cyclic groups of order $n$.

The group denoted by ${\mathbb{Z}}_n$ is always meant in conjuction with the operation $\oplus$ modulo $n$.

This group ${\mathbb{Z}}_n$ also only contains the positive numbers up to $n$ $\{0,1,2,\dots ,n-1\}$ as the negatives $\{-n+1,\dots ,-2,-1\}$ are equal a positive number ${\equiv }_n$.

Generators of $⟨{\mathbb{Z}}_n;\oplus ⟩$

The group $⟨{\mathbb{Z}}_n;\oplus ⟩$ is cyclic for every $n$, where $1$ is a generator. The generators of $⟨{\mathbb{Z}}_n;\oplus ⟩$ are all $g\in {\mathbb{Z}}_n$, $g$ coprime to $n$, i.e. for which $\text{gcd}(g,n)=1$.

Commutativity of $⟨{\mathbb{Z}}_n;\oplus ⟩$

The group $⟨{\mathbb{Z}}_n;\oplus ⟩$ is abelian.

Order of Subgroups

5.8 Lagrange's Theorem

Let $G$ be a finite group and let $H$ be a subgroup of $G$. Then the order of $H$ divides the order of $G$, i.e., $|H|$ divides $|G|$.

5.9 The order of every element divides the group order

For a finite group $G$, the order of every element divides the group order, i.e., $\text{ord}(a)$ divides $|G|$ for every $a\in G$.

Proof We have $⟨a⟩$ a subgroup of $G$ of order $\text{ord}(a)$, which according to Theorem 5.8 must divide $|G|$.

Order of a generated group

We have the order $\text{ord}(a)=|⟨a⟩|$.

5.10 Element to the power of the order is neutral

Let $G$ be a finite group. Then $a^{|G|}=e$ for every $a\in G$.

Proof $|G|=k\cdot \text{ord}(a)$ for some $k$ by Corollary 5.9. Thus $a^{|G|}=a^{k\cdot \text{ord}(a)}=(a^{\text{ord}(a)}{)}^k=e^k=e$.

5.11 Prime order cyclic groups

Every group of prime order is cyclic, and in such a group every element except the neutral element is a generator.

Proof Only $1|p$ and $p|p$ for $p$ prime, thus only a generator for an $a\in G$, with $\text{ord}(a)=1$ or $\text{ord}(a)=p$ can divide $|G|$. In the first case, $a=e$ and in the latter case $|G|=⟨a⟩$.

Euler’s Totient function

5.16 Multiplicative Group over $\mathbb{Z}$

${\mathbb{Z}}_m^{\ast }\stackrel{\text{def}}{=}\{a\in {\mathbb{Z}}_m|\text{gcd}(a,m)=1\}$

${\mathbb{Z}}_m$ (group with $\oplus$) is not a group with respect to multiplication modulo $m$, as elements that are not coprime to $m$ don’t have an inverse. Thus we need ${\mathbb{Z}}_m^{\ast }$ to remove all of these elements and have a group with $\odot$.

5.17 Euler's Totient function

The Euler function $\phi :{\mathbb{Z}}^{+}\to {\mathbb{Z}}^{+}$ is defined as the cardinality of ${\mathbb{Z}}_m^{\ast }$: $\phi (m)=|{\mathbb{Z}}_m^{\ast }|$

5.12 Euler function from prime factorisation

If the prime factorisation of $m$ is $m={\prod }_{i=1}^r{p}_i^{e_i}$, then $\phi (m)={\prod }_{i=1}^r(p_i-1)p_i^{e_i-1}$

This comes from the fact that for prime $p$ and $e\ge 1$ we have $\phi (p^e)=p^{e-1}(p-1)$since exactly every $p$th integer in ${\mathbb{Z}}_{p^e}$ contains a factor $p$ and thus $p^{e-1}(p-1)$ elements don’t contain a factor $p$, i.e. are in ${\mathbb{Z}}_{p^e}^{\ast }$. Since the $p$‘s are pairwise relatively prime (obviously) by the CRT we have that $\phi (m)=\phi (p_1^{e_1})\cdot \dots \cdot \phi (p_i^{e_i})$. This holds as the CRT allows us to establish a bijection between each $a\in {\mathbb{Z}}_m$ and a unique tuple $(a_1,\dots ,a_r)$ where $a_i{\equiv }_{p_i^{e_i}}a$.

Number of divisors of $n$

We can use a similar function to count the number of divisors of a number $n$. Write $n={\prod }_{i=1}^m{p}_i^{e_i}$. Then ${\#}_{\text{div}(n)}={\prod }_{i=1}^m(e_i+1)$

5.13 Multiplicative group ${\mathbb{Z}}_m^{\ast }$

$⟨{\mathbb{Z}}_m^{\ast };\odot ,{}^{-1},1⟩$ is a group.

Proof Idea: This holds as for $a,b\in {\mathbb{Z}}_m^{\ast }$, $\gcd (a,m)=1$ and $\gcd (b,m)=1$, thus $\gcd (ab,m)=1$. Thus this group is closed.

5.14 Fermat's Little Theorem

For all $m\ge 2$ and all $a$ with $\gcd (a,m)=1$, $a^{\phi (m)}{\equiv }_{m}1$ In particular, for every prime $p$ and every $a$ not divisible by $p$, $a^{p-1}{\equiv }_{p}1$

Proof Idea This follows from Corollary 5.10 that $a^{\text{ord}(G)}=1$ and the order of ${\mathbb{Z}}_m^{\ast }$ is $\phi (m)$ is $p-1$ for $p$ prime.

5.15 Condition for a group to be Cyclic

The group ${\mathbb{Z}}_m^{\ast }$ is cyclic if and only if $m=2$, $m=4$, $m=p^e$ or $m=2p^e$ where $p$ is an odd prime and $e\ge 1$.

RSA

$e$-th Roots in a Group

5.16 Roots in a group

Let $G$ be some finite group (multiplicatively written) and let $e\in \mathbb{Z}$ be relatively prime to $|G|$. The function $x\to x^e$ is a bijection and the (unique) $e$-th root of $y\in G$, namely $x\in G$ satisfying $x^e=y$ is $x=y^d$ where $d$ is the multiplicative inverse of $e$ modulo $|G|$, i.e. $ed{\equiv }_{|G|}1$

Proof Idea We have $ed=k\cdot |G|+1$ for some $k$ (as $ed{\equiv }_{|G|}1$). Thus for any $x\in G$ we have $(x^e{)}^d=x^{ed}=x^{k\cdot |G|+1}=(x^{|G|}{)}^k\cdot x=1\cdot x=x$ as $x^{|G|}=1$ in the group $G$.

The important reason why RSA works is that if $|G|$ is known, then $d$ can be computed from $ed{\equiv }_{|G|}$ by using the extended euclidean algorithm. If we don’t know the order of the group we have to try all possibilities.

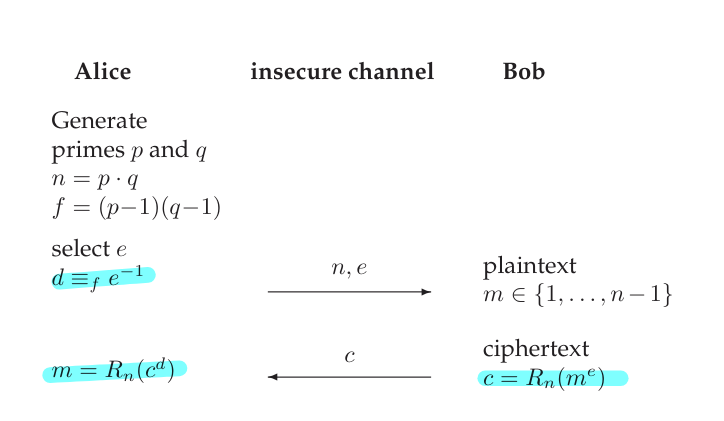
Description of RSA

Let $p$ and $q$ be two sufficiently large secret primes, where $n=pq$ the product. The order of ${\mathbb{Z}}_n^{\ast }$ $|{\mathbb{Z}}_n^{\ast }|=\phi (n)=(p-1)(q-1)$ can be computed only if the prime factors are known. Otherwise, we have to try all possibilities, i.e. all elements in the group.

Public Encryption works like this: $m\to c=R_n(m^e)$and the secret decryption is defined as $c\to m=R_n(c^d)$ where $d$ can be computed according to $ed{\equiv }_{(p-1)(q-1)}1$. (we have to choose an $e$ which is coprime to $n$ as otherwise it has no multiplicative inverse).

5.5 Rings and Fields

We now consider algebraic systems with two binary operations, usually called addition and multiplication.

Ring

5.18 Ring definition

A ring $⟨R;+,-,0,\cdot ,1⟩$ is an algebra for which:

1. $⟨R;+,-,0⟩$ is a commutative group.
2. $⟨R;\cdot ,1⟩$ is a monoid.
3. $a(b+c)=(ab)+(ac)$ and $(b+c)a=(ba)+(ca)$ for all $a,b,c\in R$ (left and right distributive laws). A ring is called commutative if multiplication is commutative ($ab=ba$).

Example $\mathbb{Z},\mathbb{Q},\mathbb{R}$ and $\mathbb{C}$ are (commutative) rings.

5.17 Ring Properties

For any ring $⟨R;+,-,0,\cdot ,1⟩$, and for all $a,b\in R$:

1. $0a=a0=0$
2. $(-a)b=-(ab)$
3. $(-a)(-b)=ab$
4. If $R$ is non-trivial (if it has more than one element), then $1\ne 0$.

0 has no multiplicative inverse, as $0a=1$ is not possible according to (1). Therefore, requesting $⟨R;\cdot ,1⟩$ to be a group would make no sense.

5.19 Characteristic of a ring

The characteristic of a ring is the order of $1$ in the additive group if it is finite, and otherwise it’s $0$ (not $\infty$!).

Example The characteristic of ${\mathbb{Z}}_m$ is $m$ as we can easily see.

Units and Multiplicative Groups

We can now impose some addition constraints onto the elements to get more interesting properties.

5.20 Units

An element $u$ of a ring $R$ is called a unit if $u$ is invertible, i.e. $uv=vu=1$ for some $v\in R$. (We write $v=u^{-1}$.) The set of units of $R$ is denoted by $R^{\ast }$.

Example The units of $\mathbb{Z}$ are $-1$ and $1$. Therefore ${\mathbb{Z}}^{\ast }=\{-1,1\}$. In contrast, ${\mathbb{R}}^{\ast }=\mathbb{R}\backslash \{0\}$, as we can divide any two numbers.

5.1 Multiplicative group $R^{\ast }$

For a ring $R$, $R^{\ast }$ is a group (the multiplicative group of units of $R$).

This holds as we can easily see that every element of $R^{\ast }$ has an inverse by definition. Thus the axiom $G3$ holds.

Divisors

Now, $R$ is a commutative ring.

5.21 Division

For $a,b\in R$ (commutative), we say that $a$ divides $b$, denoted $a|b$ if there exists a $c\in R$ such that $b=ac$. In this case $a$ is called a divisor of $b$ and $b$ is a multiple of $a$.

Every non-zero element is a divisor of $0$. Moreover, $1$ and it’s inverse $-1$ are divisors of every element.

5.19 Division properties

In any commutative ring:

1. If $a|b$ and $b|c$ then $a|c$, i.e. the relation $|$ is transitive.
2. If $a|b$ then $a|bc$ for all $c$.
3. If $a|b$ and $a|c$, then $a|(b+c)$.

We can then generalise the $\gcd$ to any commutative ring.

5.22 GCD

For any ring elements $a$ and $b$ in $R$ (not both $0$), a ring element $d$ is called a greatest common divisor of $a$ and $b$ if $d$ divides both $a$ and $b$ if every common divisor of $a$ and $b$ divides $d$, i.e. if $d|a\wedge d|b\wedge \forall c((c|a\wedge c|b)\to c|d)$

Zerodivisors and Integral Domains

5.23 Zerodivisor

An element $a\ne 0$ of a commutative ring $R$ is called a zerodivisor if $ab=0$ for some $b\ne 0$ in $R$.

5.24 Integral Domain

An integral domain $D$ is a (nontrivial, $0\ne 1$) commutative ring without zerodivisors: For all $a,b\in D$ we have $ab=0⟹a=0\vee b=0$.

Examples $\mathbb{Z},\mathbb{Q},\mathbb{R},\mathbb{C}$ are integral domains. ${\mathbb{Z}}_m$ is not an integral domain if $m$ is not a prime, as every element not relatively prime to $m$ is a zerodivisor.

5.20 Integral Domain divison

In an integral domain, if $a|b$ then $c$ with $b=ac$ is unique (and is denoted by $c=\frac{b}{a}$ or $c=b/a$ and called quotient).

Polynomial Rings

5.25 Polynomial Rings

A polynomial $a(x)$ over a commutative ring $R$ in the indeterminate $x$ is a formal expression of the form $a(x)=a_d{x}^d+a_{d-1}{x}^{d-1}+\cdots +a_{1}x+a_0={\sum }_{i=0}^d{a}_i{x}^i$ for some non-negative integer $d$, with $a_i\in R$.

The degree of $a(x)$, denoted $\mathrm{deg}(a(x))$, is the greatest $i$ for which $a_i\ne 0$.

The special polynomial $0$ (i.e., all the $a_i$ are $0$) is defined to have degree “minus infinity”.

Let $R[x]$ denote the set of polynomials (in $x$) over $R$.

The degree of the special polynomial $0$, for which all coefficients are $0$ is $\mathrm{deg}(0)=-\infty$.

A polynomial can also be understood as a simple list of coefficients, which doesn’t correspond to a function.

Degree of sum and multiplication

The degree of the:

1. sum of two polynomials is at most the maximum of their degrees, i.e. it can only be equal or smaller.
2. product of two polynomials is at most the sum of their degrees. It’s equal if $R$ is an integral domain (as otherwise $a_i{b}_i=0$ for the highest coefficient).

5.21 Commutative Ring Polynomials

For any commutative ring $R$, $R[x]$ is a commutative ring.

5.22 Polynomials over integral domains

Let $D$ be an integral domain. Then

1. $D[x]$ is an integral domain.
2. The degree of the product is the sum of their degrees.
3. The units of $D[x]$ are the constant polynomials that are units of $D$: $D[x{]}^{\ast }=D^{\ast }$.

Fields

5.26 Fields

A field is a nontrivial commutative ring $F$ in which every nonzero element is a unit, i.e. $F^{\ast }=F\setminus \{0\}$.

Fields

In other words, a ring $F$ is a field if and only if $⟨F\setminus \{0\};\cdot ,{}^{-1},1⟩$ is an abelian group.

Examples $\mathbb{Q},\mathbb{R},\mathbb{C}$ are fields, while $\mathbb{Z}$ and $R[x]$ (for any ring $R$) are not fields.

5.23 ${\mathbb{Z}}_p$ field

${\mathbb{Z}}_p$ is a field if and only if $p$ is prime.

Galois Fields

We denote the field with $p$ (thus $p$ has to be prime) elements by $\text{GF}(p)$ rather than ${\mathbb{Z}}_p$.

In a field you cannot only add, subtract and multiply but also divide by any nonzero element. This is because in a field, the multiplicative monoid is also a group (without $0$).

5.24 Field Integral domain

A field is an integral domain.

5.6 Polynomials over a Field

5.6.1 Factorisation and Irreducible Polynomials

In the integers, we have the dual divisors $1$ and $-1$. In a field, this corresponds to all constant multiples of a polynomial dividing another.

Division in Fields

If $b(x)$ divides $a(x)$, then so does $v\cdot b(x)$ for any nonzero $v\in F$. This holds because if $a(x)=b(x)\cdot c(x)$, then $a(x)=vb(x)\cdot (v^{-1}c(x))$.

5.27 Monic Polynomials

A polynomial $a(x)$ is called monic if the leading coefficient is $1$.

5.28 Irreducibility

A polynomial $a(x)\in F[x]$ with degree at least $1$ is called irreducible if it is divisible only by constant polynomials (of $\mathrm{deg}=0$) and by constant multiples of $a(x)$ (itself).

This has a couple implications:

• Every polynomial of degree $1$ is irreducible.
• A polynomial of degree $2$ is either irreducible or the product of two polynomials of degree $1$.
• A polynomial of degree $3$ is either irreducible, or it has at least a factor of degree $1$.
• A polynomial of degree $4$ is either irreducible, or it has a factor of degree $1$ or has an irreducible factor of degree $2$.

Irreducibility check

We can check if a polynomial of degree $d$ is irreducible, by checking all monic irreducible polynomials of degree $\le d/2$ as possible divisors.

GCD in a polynomial field

The monic polynomial $g(x)$ of largest degree such that $g(x)|a(x)$ and $g(x)|b(x)$ is called the greatest common divisor of $a(x)$ and $b(x)$ denoted $\gcd (a(x),b(x))$.

Because a field is an Integral Domain, $F[x]$ is also an integral domain. Therefore, we can also divide any two polynomials: $a\cdot b=a\cdot c⟹b=c$ (for $a\ne 0$).

Division property

Because the ring $F[x]$ has strong similarities to the integers $\mathbb{Z}$ there is also the division property here.

The analogy to $0\le r<|d|$ in a polynomial ring $F[x]$ is the degree, which measures the “size” of the remainder.

5.25 Division

Let $F$ be a field. For any $a(x)$ and $b(x)\ne 0$ in $F[x]$ there exists a unique $q(x)$ (the quotient) and a unique $r(x)$ (the remainder) such that $a(x)=b(x)\cdot q(x)+r(x)\text{and}\mathrm{deg}(r(x))<\mathrm{deg}(b(x))$

We denote $R_m(a)$ as $R_{m(x)}(a(x))$ in the polynomial version.

Analogies between $\mathbb{Z}$ and $F[x]$, Euclidean Domains *

TODO

5.7 Polynomials as functions

We can interpret a polynomial $a(x)$ in a ring $R[x]$ as a function $R\to R$ that evaluates the polynomial at $a(x)$ at $\alpha \in R$.

5.28 Polynomial evaluation

Polynomial evaluation is compatible with the ring operations:

• If $c(x)=a(x)+b(x)$ then $c(\alpha )=a(\alpha )+b(\alpha )$ for any $\alpha$
• f $c(x)=a(x)\cdot b(x)$ then $c(\alpha )=a(\alpha )\cdot b(\alpha )$ for any $\alpha$

Roots

5.33 Roots

Let $a(x)\in R[x]$. An element $\alpha \in R$ for which $a(\alpha )=0$ is called a root of $a(x)$.

5.29

For a field $F$, $\alpha \in F$ is a root of $a(x)$ if and only if $x-\alpha$ divides $a(x)$.

This means that an irreducible polynomial of degree $\ge 2$ has no roots.

5.30 Irreducibility and roots

A polynomial $a(x)$ of degree $2$ or $3$ over a field $F$ is irreducible if and only if it has no root.

This doesn’t work for polynomials of higher degrees as for example a polynomial of degree $4$ might be composed of $2$ irreducible polynomials of degree $2$.

5.31 Number of Roots

For a field $F$, a nonzero polynomial $a(x)\in F[x]$ of degree $d$ has at most $d$ roots.

5.7.3 Polynomial Interpolation

A polynomial over $\mathbb{R}$ of degree $d$ can be interpolated from any $d+1$ values. The same is true for any field.

5.32 Determine a polynomial

A polynomial $a(x)\in F[x]$ of degree at most $d$ is uniquely determined by any $d+1$ values of $a(x)$, i.e. by $a({\alpha }_1),\dots ,a({\alpha }_{d+1})$ for any distinct ${\alpha }_1,\dots ,{\alpha }_{d+1}\in F$.

Interpolate a polynomial from $d+1$ values

Let ${\beta }_i=a({\alpha }_i)$ for $i=1,\dots ,d+1$. Then $a(x)$ is given by Lagrange’s Interpolation formula: $a(x)={\sum }_{i=1}^{d+1}{\beta }_i{u}_i(x)$ where the polynomial $u_i(x)$ is given by $u_i(x)=\frac{(x-{\alpha }_i)\dots (x-{\alpha }_{i-1})(x-{\alpha }_{i+1})\dots (x-{\alpha }_{d+1})}{({\alpha }_i-{\alpha }_1)\dots ({\alpha }_i-{\alpha }_{i-1})({\alpha }_i-{\alpha }_{i+1})\dots ({\alpha }_i-{\alpha }_{d+1})}$

Note that for $u_i(x)$ to be well-defined, all constant terms ${\alpha }_i-{\alpha }_j$ in the denominator must be invertible. This is guaranteed in a field since $a_i-a_j\ne 0$ for $i\ne j$ (as they are all distinct).

This $a(x)$ is unique since if there was another $a^{\prime }(x)$ then $a(x)-a^{\prime }(x)$ would have at most degree $d$ and thus at most $d$ roots. But since $a(x)-a^{\prime }(x)$ has the same $d+1$ roots, it’s $0⟹a(x)=a^{\prime }(x)$.

5.8 Finite Fields

The Ring $F[x{]}_{m(x)}$

In the same ways as there is $\mathbb{Z}$ and ${\mathbb{Z}}_m$, there is also $F[x]$ and $F[x{]}_{m(x)}$.

Modulo in the Field

$a(x){\equiv }_{m(x)}b(x)\stackrel{\text{def}}{\iff }m(x)|(a(x)-b(x))$

5.33 Congruence

Congruence modulo $m(x)$ is an equivalence relation on $F[x]$, and each equivalence class has a unique representation of degree less than $\mathrm{deg}(m(x))$.

Example In $\text{GF}(2)[x]$ we have $x^4+x^3+x^2+1{\equiv }_{x^2+1}x+1$

5.34 Definition of $F[x{]}_{m(x)}$

Let $m(x)$ be a polynomial of degree $d$ over $F$. Then $F[x{]}_{m(x)}\stackrel{\text{def}}{=}\{a(x)\in F[x]|\mathrm{deg}(a(x))<d\}$

5.34 Cardinality of finite field

Let $F$ be a finite field with $q$ elements and let $m(x)$ be a polynomial of degree $d$ over $F$. Then $|F[x{]}_{m(x)}|=q^d$. This is the amount of combinations we have for $d$ coefficients and $q$ possible elements.

5.35 Ring properties of $F[x{]}_{m(x)}$

$F[x{]}_{m(x)}$ is a ring with respect to addition and multiplication modulo $m(x)$.

5.36 Inverses

The congruence equation $a(x)b(x){\equiv }_{m(x)}1$ for a given $a(x)$ has a solution $b(x)\in F[x{]}_{m(x)}$ if and only if $\gcd (a(x),m(x))=1$. The solution is unique. In other words, $F[x{]}_{m(x)}^{\ast }=\{a(x)\in F[x{]}_{m(x)}|\gcd (a(x),m(x))=1\}$

This is a very similar structure to the group ${\mathbb{Z}}_m^{\ast }$.

Constructing Extension Fields

5.37 Field $F[x{]}_{m(x)}$

The ring $F[x{]}_{m(x)}$ is a field if and only if $m(x)$ is irreducible, i.e. it’s $\gcd$ is $1$ with every polynomial in $F[x{]}_{m(x)}$. This means that all elements are units (except $0$).

Example $\mathbb{R}[x{]}_{x^2+1}$ is a field, isomorphic to $\mathbb{C}$. There are no other extension fields on $\mathbb{R}$ with irreducible polynomials $m(x)$ that aren’t isomorphic to $\mathbb{C}$.

Some Facts about finite Fields *

When $F$ is a finite field, so is $F[x{]}_{m(x)}$ for a given polynomial $m(x)$.

5.38 Galois Fields

For every prime $p$ and every $d>1$ there exists an irreducible polynomial of degree $d$ in $\text{GF}(p)[x]$. In particular, there exists a finite field with $p^d$ elements.

5.39

There exists a finite field with $q$ elements if only if $q$ is a power of a prime. Moreover, any two finite fields of the same size $q$ are isomorphic.

5.40 Cyclic Multiplicative groups

The multiplicative group of every finite field $\text{GF}(q)$ is cyclic.

This group has order $q-1$ and $\phi (q-1)$ generators.

5.9 Application: Error-Correcting Codes

5.9.1 Encoding

5.35 $(n,k)$-encoding function

An $(n,k)$-encoding function $E$ for some alphabet $\mathcal{A}$ is an injective function that maps a list $(a_0,\dots ,a_{k-1})\in {\mathcal{A}}^k$ of $k$ (information) symbols to a list $(c_0,\dots ,c_{n-1})\in {\mathcal{A}}^n$ of $n>k$ (encoded) symbols in $(A)$ called codeword: $E:{\mathcal{A}}^k\to {\mathcal{A}}^n:(a_0\dots ,a_{k-1})\to E((a_0\dots ,a_{k-1}))=(c_0,\dots ,c_{n-1})$

We call the set $\mathcal{C}=\text{Im}(E)$ the set of codewords.

5.36 Cardinality of the acode

An $(n,k)$-error-correcting code over the alphabet $\mathcal{A}$ with $|\mathcal{A}|=q$ is a subset of ${\mathcal{A}}^n$ of cardinality $q^k$.

5.37 Hamming distance

The Hamming distance between two strings of equal length over a finite alphabet $\mathcal{A}$ is the number of positions at which the two strings differ.

5.38 Minimum Distance

The minimum distance of an error-correcting code $\mathcal{C}$, denoted $d_{\text{min}}(\mathcal{C})$, is the minimum of the Hamming distance between any two codewords.

5.9.2 Decoding

5.39 Decoding function

A decoding function $D$ for an $(n,k)$-encoding function is a function $D:{\mathcal{A}}^n\to {\mathcal{A}}^k$.

A good decoding function takes an arbitrary list $(r_0,\dots ,r_{n-1})\in {\mathcal{A}}^n$ of symbols and decodes it to the most plausible information vector. It should also be efficiently computable.

5.40 $t$-error correcting

A decoding function $D$ is $t$-error-correcting for encoding function $E$ if for any $(a_0,\dots ,a_{k-1})$ $D((r_0,\dots ,r_{n-1}))=(a_0,\dots ,a_{k-1})$ for any $(r_0,\dots ,r_{n-1})$ with Hamming distance at most $t$ from $E((a_0,\dots ,a_{k-1}))$. A code is $t$-error-correcting if there exists $E$ and $D$ with $\mathcal{C}=\text{Im}(E)$ where $D$ is $t$-error-correcting.

5.41 Minimum distance

A code $\mathcal{C}$ with minimum distance $d$ is $t$-error correcting if and only if $d\ge 2t+1$.

5.9.3 Codes based on polynomial evaluation

5.42 Polynomial encoding function

Let $\mathcal{A}=\text{GF}(q)$ for some $q$ and let ${\alpha }_0,\dots ,{\alpha }_{n-1}$ be arbitrary distinct elements of $\text{GF}(q)$. We then encode the values to the polynomial evaluation by $a(x)$ with coefficients equal to the input: $E((a_0,\dots ,a_{k-1}))=(a({\alpha }_0),\dots ,a({\alpha }_{n-1}))$ This code has a minimum distance of $n-(k-1)=n-k+1$.

The polynomial (i.e. the coefficients, i.e. the message) can be interpolated from any $k$ values by Lagrangian interpolation: Two different codewords cannot agree at $k$ positions, otherwise they are equal. Thus they disagree in any $n-k+1$ positions (otherwise they’d agree in $k$ or more and thus they’d be equal).

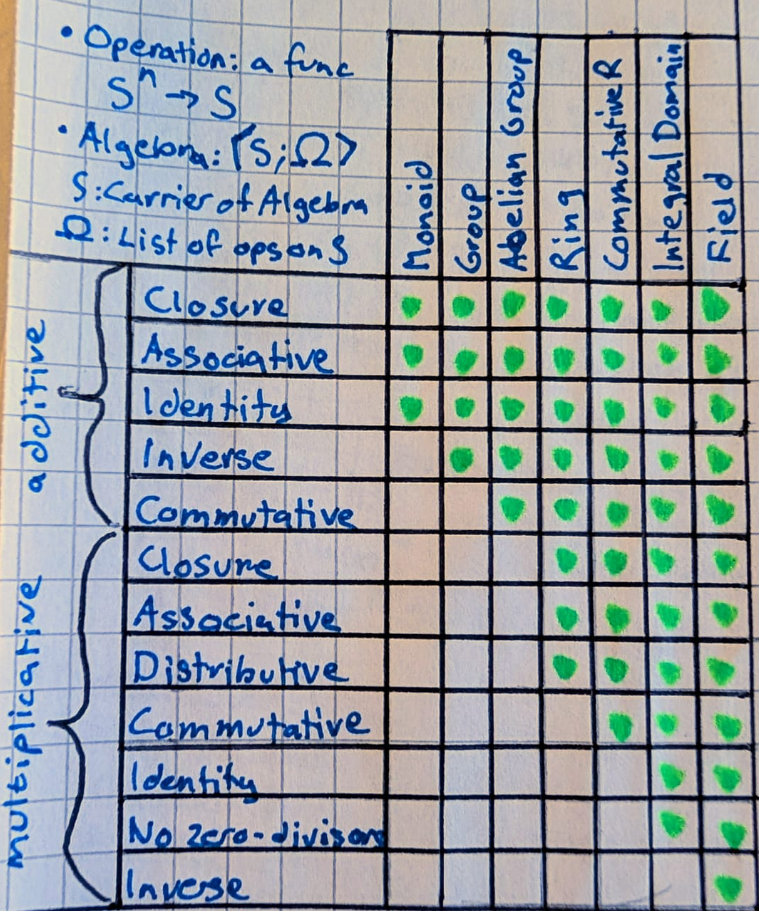
Cheatsheet

Carriers and Operations for groups

	${\mathbb{Z}}_m$	${\mathbb{Z}}_m^{\ast }$
$\oplus$	Yes	No
$\odot$	No	Yes

Rings and Fields

$R$ is a ring, $CR$ a commutative ring, $D$ an integral domain and $F$ a field.

Structure	$R$	$CR$	$D$	$F$	$R[x]$	$CR[x]$	$D[x]$	$F[x]$	$F[x{]}_{(m(x))}$	$F[x{]}_{(m(x))}^{\ast }$	$\frac{F[x]}{(m(x))}$, $m(x)$ irred.
Ring	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
Comm. Ring	—	✓	✓	✓	—	✓	✓	✓	✓	✓	✓
Integral Domain	—	—	✓	✓	—	—	✓	✓	—	✓	✓
Field	—	—	—	✓	—	—	—	—	—	✓	✓

Properties of the different structures

Techniques

Polynomial division

See Week 10 DM Übung in Goodnotes

If the polynomial we are dividing by is not monic, i.e. we have $3x^2+6x+5$ divided by $4x+2$ in $GF(7)[X]$, we can use the inverse of $4$ modulo $7$ to reduce it to one. $4\cdot 2{\equiv }_{7}1$ thus $3\cdot 2\cdot (4x+2){\equiv }_{7}3x^2+5$.

Find Zero-Divisors in $GF(q)[x{]}_{m(x)}$

We find the factorisation of $m(x)$. All multiplies of the factors of $m(x)$ are thus zero-divisors.

Example: Consider the ring $\text{GF}[3{]}_{x^2+2}$. We can write $x^2+2=x^2-1=(x+1)(x-1)=(x+1)(x+2)$ as $2{\equiv }_3-1$. Thus all zerodivisors are the multiples of $x+1$ and $x+2$:

• $x+1$, $2x+2$
• $x+2$, $2x+1$

Find GCD of two polynomials

We need to find a common factor $(x-\alpha )$ using the roots (Nullstellen) method by trying all possible elements of the $GF(n)$. Then we use the division with remainder to find the smaller elements and here we repeat the method used before.

We cannot just find all roots (Nullstellen) and let that be the gcd, as there might be a “double”-root: $a(x)=(x+1)(x+1)(x+2)$ where the gcd is not $(x+1)$ but $(x+1)(x+1)$ that we wouldn’t have noticed just by the roots.