0. Layered Graphs

In practice, instead of modifying the search algorithm, we want to modify the graph (so we don’t have to re-invent the wheel).

This means that when we have a graph-traversal problem such as searching for a cheapest path, we want to build in the constraints into our graph by layering it. The edges between layers then represent state transitions.

Idea

Let’s look at an example. We are looking at a direct graph with non-negative edge-weights. Instead of a normal traversal, we are also allowed to cheat, up to $k$ times. Cheating means setting the weight of an edge to $0$.

The idea is to create $k+1$ different layers in our graph, each representing having cheated $i$ times where $i\in [k]$. Each layer is connected normally, with non-modified edge-weights. There is also an edge of weight $0$ from every vertex to it’s successor in the next layer $i+1$.

To cheat, you can use a downwards edge that links a graph with $i$ cheats to one with $i+1$ cheats. Because there are no upwards edges, you cannot “un-cheat”.

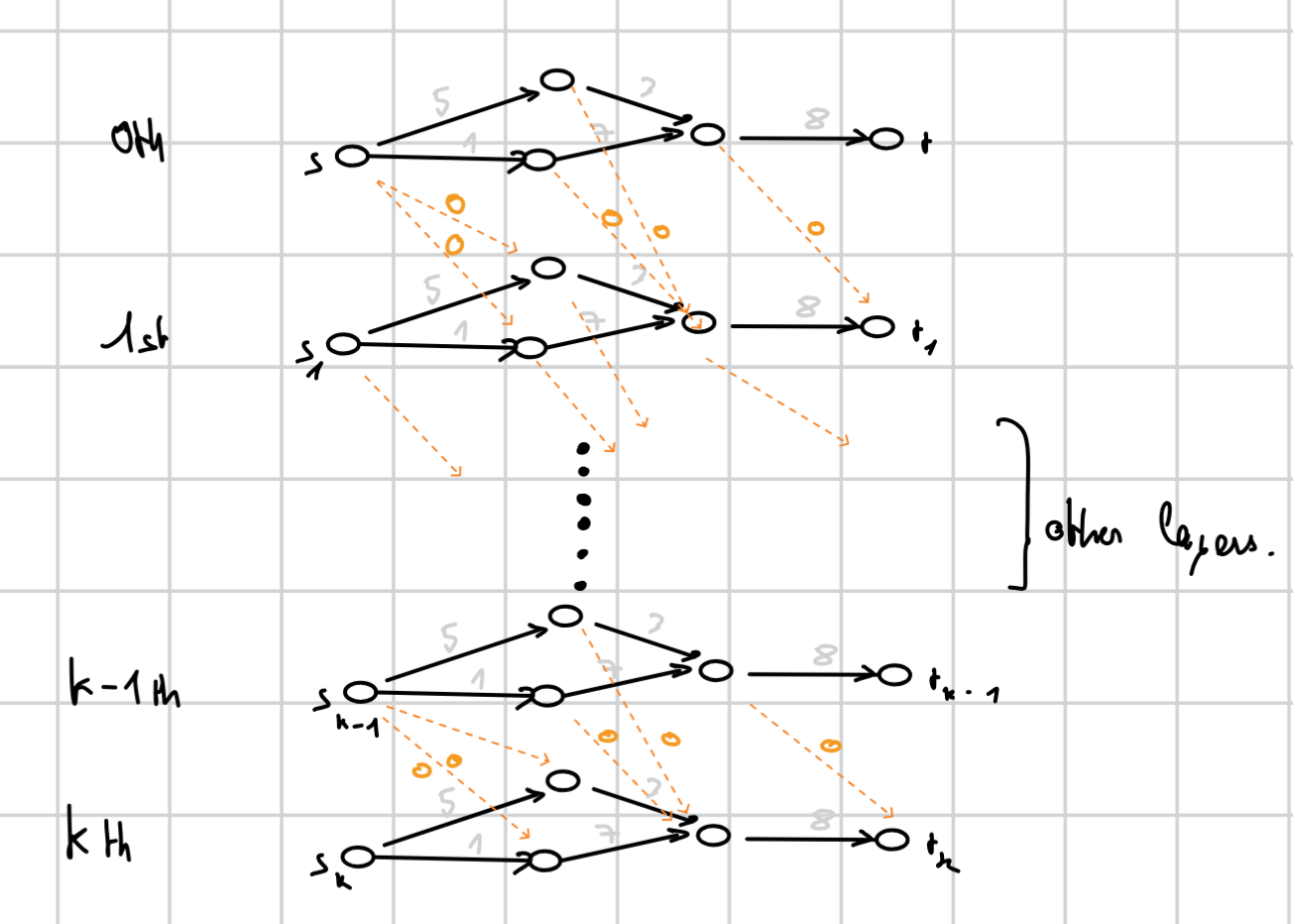
To find the shortest path, we can apply Dijkstra’s to this graph. We then take the minimum over the distances to all $t_i$ for $i\in [k]$. We could also link all $t_i$ edges together with cost $0$ instead of looping over the target vertices.

Formalising

To define the vertices:

1. Use a direct product between the set of vertices and our $k$ cheats: $V^{\prime }=V\times 0,\dots ,k$.
2. Use super- or subscript: $V^{\prime }=\{v^{(\ell )}:v\in V,\ell \in \{0,1,2,...,k\}\}$

This new vertex set has size $|V^{\prime }|=(k+1)\cdot |V|$.

To define the edges: We can either use our set notation from before to create edges from: $\forall (v,w)\in E,0\le i\le k:(\{v,i\},\{w,i\})\in E^{\prime }$.

Or we define $E^{\prime }$ and $c^{\prime }:E^{\prime }\to {\mathbb{R}}_{\ge 0}$ by $(T1)$: $\forall (v,w)\in E,0\le \ell \le k:(v^{(\ell )},w^{(\ell )})\in E^{\prime }\text{ with }{c}^{\prime }((v^{(\ell )},w^{(\ell )}))=c((v,w))$And our edges from one layer to the next with cost $0$ $(T2)$: $\forall (v,w)\in E,0\le \ell \le k-1:(v^{(\ell )},w^{(\ell +1)})\in E^{\prime }\text{ with }{c}^{\prime }((v^{(\ell )},w^{(\ell +1)}))=0$ The first set of edges $(T1)$ represents normal edge-traversal in $G$, the second set $(T2)$ represents cheating, and the final set $(T3)$ ensures that there is always a path from $s^{(0)}$ to $t^{(k)}$ in $G^{\prime }$ if there is a path from $s$ to $t$ in $G$.