10. All-Pairs Shortest Path

The All-Pairs Shortest Path problem addresses the fact that previously we only computed the shortest paths from a start vertex $s$ to all others.

The naive way to do this would be to run our known algorithms $|V|$ times, once for each possible source vertex:

Cost Function	Algorithm	Runtime
$c(e)=1$	BFS repeated	$O(n(m+n))$
$c(e)\ge 0$	Dijkstra’s repeated	$O(n(m+n)logn)$
$c(e)\in \mathbb{R}$	Bellman-Ford repeated	$O(n^2\cdot m)$
Note that if we have $m=\Theta (n^2)$ for a fully connected graph, BF gives $O(n^4)$.

Floyd-Warshall

Restrictions: No negative Cycles Runtime: $O(|V{|}^3)$

Floyd-Warshall utilises dynamic programming to calculate the shortest paths more effectively. Once the DP-Table has been computed, we can query it for efficient lookups.

Recurrence

Consider a graph with vertices $V=\{1,2,\dots ,n\}$. Our subproblem is: ”$d_{u\to v}^{(k)}:=$ shortest path from $u$ to $v$ passing only vertices with index $\le k$“. (This gives us a 3D DP table.)

There are three options in the recurrence here:

1. The path uses the vertex $k$ as it’s shorter: $d_{u\to v}^{(k)}=d_{u\to v}^{(k-1)}$
2. The path uses vertex $k$ exactly once: $d_{u\to v}^{(k)}=d_{u\to k}^{(k-1)}+d_{k\to v}^{(k-1)}$
3. The path uses $k$ more often (only worth it if $k$ is in a negative cycle thus we ignore it)

Our base case is $i=0$:

1. If $u=v$: $d_{u\to v}=0$
2. If $u\ne v$:
   1. If $uv\in E$: $d_{u\to v}=c(u,v)$
   2. Otherwise $d_{u\to v}=\infty$

Implementation (Bottom-Up)

We can optimise the recurrence not to store the values in a 3D, but a 2D array only, by keeping only the last values.

The best way to store the edges and their costs is in a Adjacency Matrix, as this allows the fastest lookup, which is the only needed operation here.

def FloydWarshall(V, E, c):
    n = len(V)
    d = [[float('inf')] * n for _ in range(n)]  # Initialize distances to infinity
 
    # Base Cases: Distance to self is 0, direct edge costs
    for u in V:
        d[u-1][u-1] = 0
        for v in V:
            if (u, v) in E:
                d[u-1][v-1] = c((u, v))
 
    # Main Dynamic Programming Loop
    for k in range(1, n + 1):         # Intermediate vertices allowed (1 to n)
        for i in range(1, n + 1):     # Source vertex
            for j in range(1, n + 1): # Destination vertex
                d[i-1][j-1] = min(d[i-1][j-1], d[i-1][k-1] + d[k-1][j-1])
 
    return d

Important: Use a value like 10000 instead of Integer.MAX_VALUE in Java, as you get overflows otherwise.

We can also read of the shortest paths by keeping a pred array in which we store the vertex k that lead to the update of the value. Then we can recursively reconstruct the path.

Runtime

We can read off the runtime from the 3 for loops very easily. Floyd-Warshall runs in $O(|V{|}^3)$.

Negative Cycles

Floyd-Warshall detects negative cycles in a similar way to Bellman-Ford.

Negative Cycles with Floyd-Warshall

There exists a negative cycle $\iff$ $\exists v\in V:d_{v\to v}^n<0$

In words: If there exists a path from a vertex to itself with negative weight (passing through any other vertex, i.e. after the $(n)$th iteration of the outer loop), then there exists a negative cycle that contains this vertex.

We can thus check for the existence of a negative cycle by running the following check:

# Negative Cycle Detection
for v in V:
	if d[v-1][v-1] < 0:
		return "Negative Cycle Detected"

Proof: (by contradiction)

1. Assume a negative cycle $C$ exists
2. Decompose it into a path from start-vertex $i$ to $j$ and back, where $j$ has the highest index all vertices in the cycle. This gives $P_1$ and $P_2$.
3. We can now use the subproblems (true by optimality principle of DP):
   1. $c(P_1)\ge d_{i\to j}^{(j-1)}$
   2. $c(P_2)\ge d_{j\to i}^{(j-1)}$
4. Thus $c(c)=c(P_1)+c(P_2)\ge d_{i\to j}^{(j-1)}+d_{j\to i}^{(j-1)}$. But because $c(C)<0$, there will be one diagonal entry $<0$.

Note: If there exists a negative cycle, but it’s not reachable from $u$ and any vertex in the cycle doesn’t reach $v$, we can ignore it and the distance will still be correct.

Johnson’s Algorithm

Runtime: $O(n\cdot (n+m)\log n)$ (exactly as fast as $n$ times Dijkstra’s, but runs on negatives) Requirements: Negative edges allowed, no negative cycles

Johnson’s increases the weight of all edges to $>0$ in order to allow Dijkstra’s to run on the graph. It does this by assigning a height $h(v)$ to each vertex. The new cost is then $\hat{c}(u,v)=c(u,v)+h(u)-h(v)$.

This means that for a path $P=(s,v_1,v_2,\dots ,v_n,t)$ the cost $\hat{c}(P)=\hat{c}(s,v_1)+\hat{c}(v_1,v_2)+\cdots +\hat{c}(v_n,t)$ the costs cancel out in pairs: $c(s,v_1)+h(s)-h(v_1)+c(v_1,v_2)+h(v_1)-h(v_2)+\cdots +c(v_n,t)+h(v_n)-h(t)$ gives $=c(P)+h(s)-h(t)$. This is called a telescoping sum.

Naive Approach

Why adding a constant to each edge (equal to the lowest negative edge as to make it 0) doesn’t work: A longer path (more edges) would get increased in cost more than a shorter. This is not what we want, we want the ordering to stay the same. Thus we need the cost to only depend on the start- and end-vertex (not on which path was taken).

How to determine the heights

We need the heights to be chosen such that the edge weights are all $>0$ which is a seemingly hard problem. Note that the system has no solution if there are negative weight cycles. These will also be reported during the B-F run and then we can abort computation.

The solution is to add a new vertex $z$ which has a directed edge of cost 0 to all vertices in the graph:

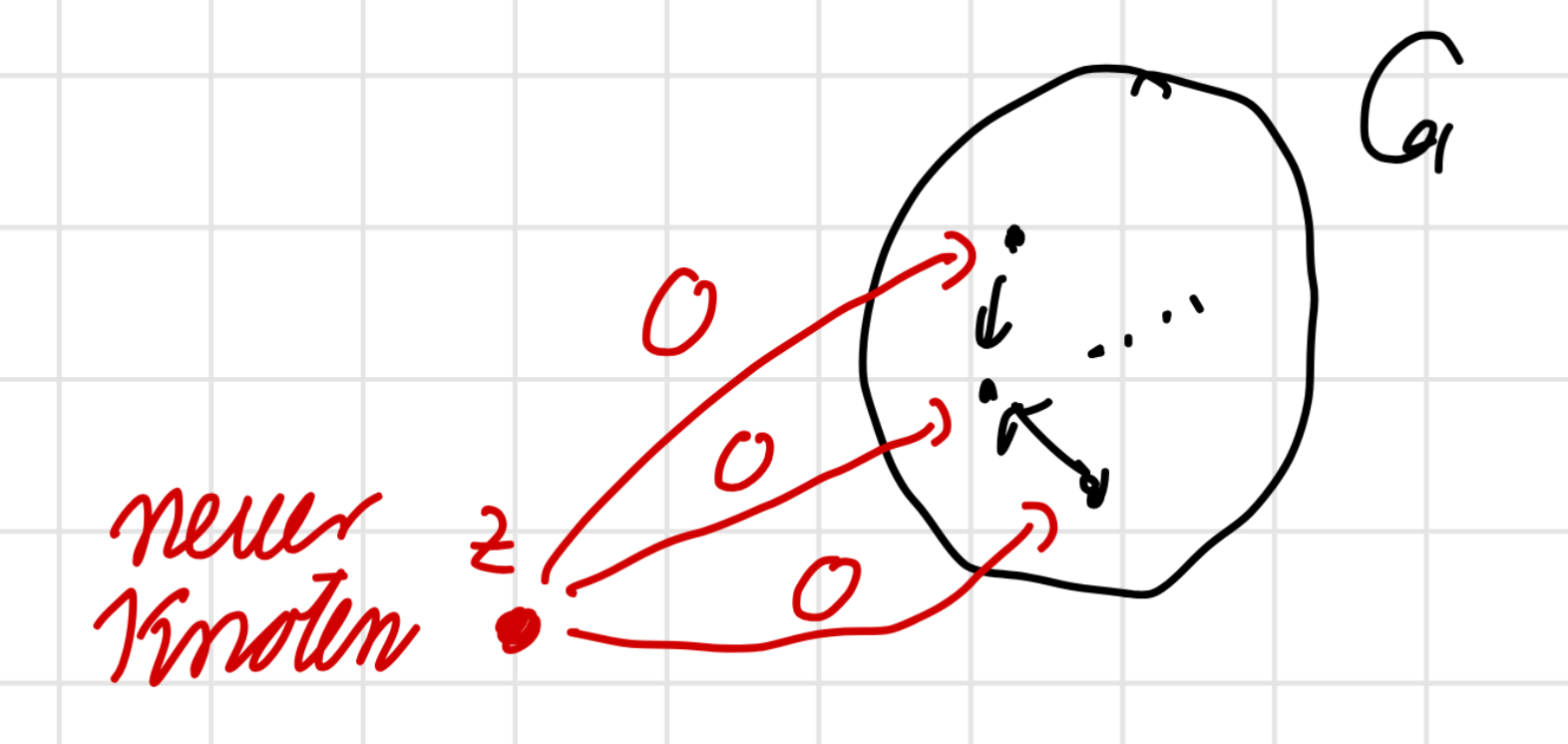
We then run B-F on the graph starting from $z$ and the height of each vertex is equal to the $h(v)=c(z,v)$. We know by the triangle inequality and the definition of shortest path: $h(v)\le h(u)+c(u,v)$which then gives us $0\le c(u,v)+h(u)-h(v)$ by rearranging, which is exactly what we want. We can now run Dijkstra’s.

Step	Runtime	Description
1. Augment Graph	$O(n)$	Add a new vertex $z$ and connect it to all existing vertices with zero-weight edges.
2. Compute Heights	$O(nm)$	Run Bellman-Ford from z to calculate the height function $h(v)$ (shortest distance from $z$ to $v$). Detect negative cycles. If a negative cycle is found, report it and terminate.
3. Reweight Edges	$O(m)$	Compute reweighted edge costs $\hat{c}(u,v)=c(u,v)+h(u)-h(v)$ for all edges $(u,v)\in E$.
4. Run Dijkstra’s	$O(n(m+nlogn))$	Run Dijkstra’s algorithm from each vertex in the reweighted graph to compute all-pairs shortest paths.
5. Undo Edge-Weights	$O(m)$	Convert the distances back to the original weights using: $d^{\prime }(u,v)=d^{\prime }(u,v)-h[u]+h[v]$

The runtime is dominated by step 2. and 4., but as $m<(m+n)\log n$, we get just Dijkstra’s runtime.

This may sound surprising, but the higher overall cost allows us to run pre-computation steps for “free”.

When to use F-W, when Johnson’s

Dense Graphs: ($m=\Theta (n^2)$, fully connected for example). Floyd-Warshall is more efficient here as the $n\cdot (n+m)$ of Johnson’s is actually $n\cdot (n+n^2)\le O(n^3)$ and thus more expensive.

Sparse Graphs: (Trees for example) Here Johnson’s shines.