2. Suchen und Sortieren

Invariants are a concept used to prove the correctness of an algorithm. By proving that the invariant holds for each iteration of the loop, we can prove that the invariant holds at the end of the algorithm. It works similarly to induction.

Search Algorithms

No search algorithm can be faster than $O (lo g (n))$ because that is the minimum amount of comparisons required to have “seen” all elements.

Linear Search

Linear search simply goes through the entire list and compares the current element to the one we are searching. The runtime is $Θ (n)$ , as it’s a single for loop.

Linear search does not require a sorted array, it will perform the same on any array.

Binary Search

For binary search, we require a sorted array.

You start in the middle and if the middle element is not the one you’re searching, you recurse on the left OR right side (depending on the middle elements size).

The runtime of binary search is optimal, it is $O (lo g (n))$ .

# Iterative implementation
def binary_search(arr[0..n-1], x):
	low = 0
	high = n - 1
	
	while low <= high:
		mid = (low + high) // 2 # floor of the middle element
		
		if arr[mid] == x:
			return mid
		else if arr[mid] < x:
			low = mid + 1 # set the search bound to be the upper half
		else:
			high = mid - 1 # set the search bound to be the lower half
	
	return -1

Sorting Algorithms

The lowest time complexity any comparison based sorting algorithm could ever have is $Ω (n lo g (n))$ !.

We know the following sorting algorithms and their runtimes:

Algorithm	Runtime (best-case)	Runtime (worst-case)
Bubble Sort	$O (n)$	$O (n^{2})$
Selection Sort	$O (n^{2})$	$O (n^{2})$
Insertion Sort	$O (n)$	$O (n^{2})$
Merge Sort	$O (n lo g (n))$	$O (n lo g (n))$
Quicksort	$O (n lo g (n))$	$O (n^{2})$
Heapsort	$O (n lo g (n))$	$O (n lo g (n))$
You need to know how each of them works, but only need to know how to implement one of the $O (n lo g (n))$ algorithms for the exam.

Bubble Sort

Attributes:

In place
Best Case: $O (n)$
Worst Case: $O (n^{2})$

Invariant “Nach $j$ Durchläufen der äusseren Schleife sind die $j$ grössten Elemente am richtigen Ort.”

Bubble sort is the easiest algorithm to understand. It goes through the array $n$ times, each time “bubbling up” the biggest element to the end, by swapping.

def bubble_sort(arr[0..n]):
	for i = 0 to n-1:
		for j = 0 to n-1-i:
			if arr[j] > arr[j + 1]:
				swap(arr[j], arr[j + 1])

During each inner iteration, high elements are swapped with their right neighbours until they hit a higher one. The algorithm then continues after that.

We use $Θ (n^{2})$ comparisons and $O (n^{2})$ switches.

The worst-case is $O (n^{2})$ performance, for an array sorted in descending order.

Selection Sort

Attributes:

In place
Best Case: $O (n^{2})$
Worst Case: $O (n^{2})$

Invariant “Nach $j$ Durchläufen der äusseren Schleife sind die $j$ grössten Elemente am richtigen Ort.” (Same as for Bubblesort).

Every iteration, selection sort goes through the “unsorted part” of the array, searches for the biggest element and puts it at the end.

def selection_sort(arr[0..n]):
	for i = 0 to n-1:
		max = MIN_VALUE
		max_index = -1
		
		for j = 0 to n-1-i:
			if arr[j] > max:
				max = arr[j]
				max_index = j
				
		tmp = arr[n-1-i]
		arr[n-1-i] = arr[max_index]
		arr[max_index] = tmp

Thus on the right-side (or left-side if inverted), we have a list of sorted integers slowly growing, while we only compare the unsorted ones to findest the next biggest to put at the beginning of the sorted list.

Insertion Sort

Attributes:

In place
Best Case: $O (n)$
Worst Case: $O (n^{2})$

Invariant “Nach $j$ Durchläufen der äusseren Schleife ist das Teilarray $A [1, \dots, j]$ sortiert (es enthält aber nicht zwangsläufig die $j$ kleinsten Elemente des Arrays).”

For insertion sort, we start at the left-side and create our sorted array there. We take the next element from the unsorted ones and insert it at the correct place in our sorted array. This insertion is not constant time! We have to swap it with each previous element!

def insertion_sort(arr[0..n]):
	for i = 1 to n:
		insertion_index = binary_search(arr, arr[i], from index 0 to 1 in arr)
		tmp1 = arr[i]
		arr[insertion_index] = arr[i]
		
		# Shift the entire array one to the right after the insertion index
		for j = insertion_index+1 to i:
			tmp2 = arr[j]
			arr[j] = tmp1
			tmp1 = tmp2

Insertion sort is slowly sorting in the elements from the right side into the left side sorted array.

Merge Sort

Attributes:

not in place, thus the space complexity is $K (n)$ . It can be programmed to be in place though.
Best Case: $O (n lo g (n))$
Worst Case: $O (n lo g (n))$

Invariant Merge sort always sorts correctly when called for a sub-array shorter than $r - l + 1$ . This means that merge has to correctly merge the two sub-arrays into a complete array.

We implement merge sort recursively as follows:

def merge_sort(arr, l, r):
	if l < r:
		mid = (l + r) / 2
		
		merge_sort(arr, l, mid) # merge sort left 
		merge_sort(arr, mid+1, r) # merge sort the right
		
		arr = merge(arr, l, mid, r) # merge them
				
# Merge together the two arrays left and right
def merge(arr, l, mid, r):
	# new array
	B = [] of length r - l + 1
	
	i = l
	j = mid + 1
	k = 0
	
	# go through the merge left and right, taking the smaller of them to create a sorted merged
	while i <= mid && j <= r:
		if arr[i] <= arr[j]:
			B[k] = arr[i]
			i++
		else:
			B[k] = arr[j]
			j++
		
		k++
		
	# append what's left immediately
	while i <= mid:
		B[k] = arr[i]
		i++
		k++
		
	# append what's left immediately (only one of the loops will actually do something, the other will already have been merged in)
	while j <= r:
		B[k] = arr[j]
		j++
		k++
		
	return B

Merge sort works by divide-and-conquering the array into smaller chunks. it then merges them together slowly.

The merging works by having two indices showing the current position in the left and right array that we are merging. We then compare the elements at the indices and take the smaller one. We then increase the counter on that array, while the other stays the same.

As soon as one array has been merged in completely, we can just append the second one (as it’s already sorted).

The worst-case scenario for Mergesort is an array that has alternating small and big elements, thus they will always have to be compared during the merge.

Quicksort

Attributes:

Not in place (but can be implemented)
Best Case: $O (n lo g (n))$
Worst Case: $O (n^{2})$

Invariant “Elemente links des pivots sind kleiner und Elemente rechts des Pivots sind größer als das Pivot-Element selbst.”

Quicksort works by taking an element as the “pivot”. We then split the array in to two parts: one smaller than the pivot and the other bigger. We then swap the pivot into the middle of that. Repeat for each of the smaller subdivisions, until you arrive at single-array elements.

We usually choose the last element (element r) as the pivot, which can go wrong if the array is already sorted. Then we only have split the array into one part, with size $n - 1$ . In the best case the pivot is exactly in the middle and we can perfectly recurse with $lo g (n)$ .

def quicksort(arr[1..n], l, r):
	if l < r:
		k = split(arr, l, r)
		
		quicksort(a, l, k-1)
		quicksort(a, k+1, r)
		
def split(arr[1..n], l, r):
	p = arr[r] # the pivot element on the right
	k = count_smaller(arr, p)
	
	B = [] * (r - l + 1) # new array for storage
	
	i = l
	j = k + 1
	
	for s in range(l, r):
		if arr[s] <= p:
			B[i] = arr[s]
			i += 1
		else:
			B[j] = arr[s]
			j += 1
			
	copy(B, arr[l, r]) # copy the B array into the subset of arr

The worst-case is if we have an array that is already sorted. If we instead randomly choose the pivot, we avoid the worst-case pitfalls.

Heapsort

Attributes:

Not in place (heap)
Best Case: $O (n lo g (n))$
Worst Case: $O (n lo g (n))$

Invariant The heap property is correct for the maxHeap. Then the biggest element will always be on top.

Heapsort works like selection sort by always selecting the largest element and placing it at the end of the sorted array, but instead of having to do an expensive linear search for the largest element, we make it $O (lo g (n))$ .

This is done by converting the array into a MaxHeap before sorting. This Heap is a tree that has the property that children are always smaller than their parents.

def heapsort(arr[1..n]):
	H = heapify(arr)
	
	for i in range(n, 1):
		A[i] = extract_max(H)

Extract Max

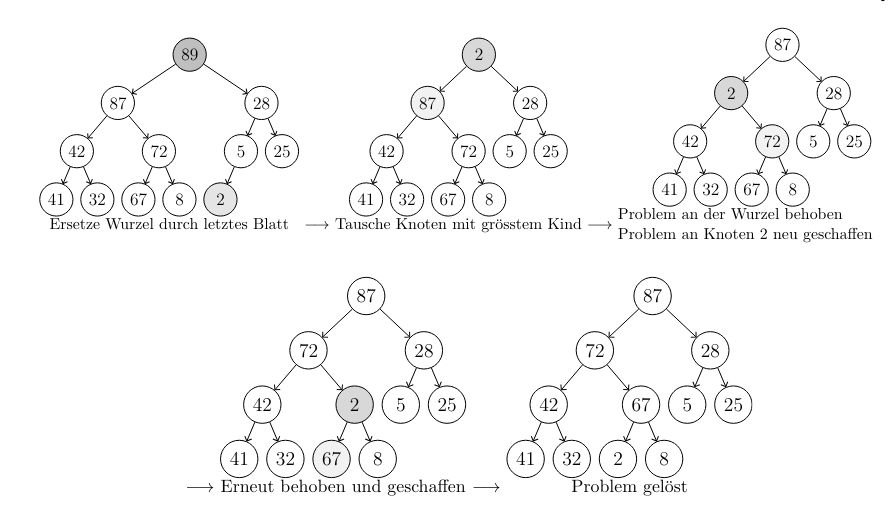
The extract max operation works by taking the root node, the biggest element in the heap by it’s definition and restoring the heap condition. We remove the root and replace it by the element that is most to the right (last element in the array storing the heap).

Then we “versickern” this small element, until the heap condition is restored. We swap it with the larger of the child nodes, until it’s bigger than both of it’s children. This takes $O (lo g (n))$ time as the tree has maximum $O (lo g (n))$ levels.

Creating the Heap

Note the property that the children of a node k in a tree are at 2k and 2k + 1. This means that the tree is stored in memory by levels.

To create the heap, we define an insert function and then use it to insert the elements in order of their appearance in the original array.

This works by inserting the node $v$ at the next free space in the tree, i.e. first to the left, then right (to conserve the tree structure).

Then we restore the heap condition by reverse-”versickern” the element until it’s restored. You swap it with it’s parent nodes until the condition is restored.

How fast can we sort

There is a lower bound for the worst-case of a comparison based sorting algorithm, which is $Ω (n lo g n)$ .

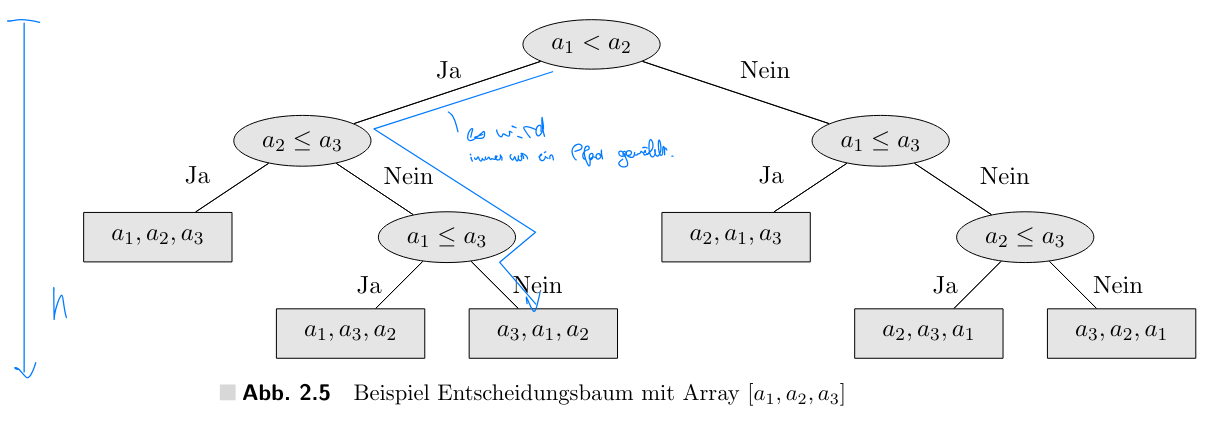
The proof is as follows:

the algorithm has to correctly sort all arrays, thus every permutation of an array.
We create a decision tree where each leaf is one permutation, while each node is a comparison of elements, which lead to the correct permutations.
In the worst-case, an algorithm has to therefore execute $h$ comparisons, where $h$ is the height of the tree.
The height of such a tree is $2^{h + 1} > n!$ permutations $\Rightarrow h > lo g_{2} (n!) - 1$ .
Since a comparison is constant time, we need $Θ (n lo g n)$ comparisons.

There are non-comparison based sorting algorithms, for example Bucketsort.

Niklas @ ETHZ

Explorer

Search Algorithms

Linear Search

Binary Search

Sorting Algorithms

Bubble Sort

Selection Sort

Insertion Sort

Merge Sort

Quicksort

Heapsort

Extract Max

Creating the Heap

How fast can we sort

Graph View

Table of Contents

Backlinks