Abstract Data Types
An ADT describes what we want to do with data, without going into implementation detail. It defines a list of operations that can be executed over an amount of data.
The datastructure itself would then be the implementation of this wish-list of operations.
ADT List
A list is an ordered collection of objects (order is relevant). The objects will be natural numbers (“Schlüssel”). One object value can appear multiple times.
Operations:
insert(k, L): insert the key K at the end of the listLget(i, L): return the memory address of thei-th key in listLdelete(k, L): remove the keykfrom the listLinsertAfter(k, k', L): Inserts the keyk'after the keykin the listL
For delete and insertAfter we could either only hand the method the key’s value or we could specify the memory address of the object. This is especially important if there’s more than one key with that value. In this lecture we’ll assume the function is handed the memory address as well.
There is also a pointer to the end of the list stored in a linked list, in an array in any case to mark the end of the data.
Implementations
| Operation | Array | Singly Linked List | Doubly Linked List |
|---|---|---|---|
insert(k,L) | |||
get(i,L) | |||
insertAfter(k,k',L) | |||
delete(k,L) | |||
| We assume to have a pointer to the end of the list here. |
Array
If we have an upper bound for the size of the list, we can use the data structure array. If the array is not full, the rest of the cells are empty (garbage / null data).
- We can
insertin as we know the first empty cell in the array and can just write the key there. getis as well, since we know where the keykis stored in memory (offset).insertAfteris since we have to shift the entire contents of the array behind the newly inserted element by 1.deleteis also in the worst case as we need to shift all contents of the array left of the deleted item by 1.
Singly Linked List (einfach verkettete Liste)
A singly linked list is a dynamic data structure in which the elements of the list don’t appear in order in memory, instead each one stores a pointer to the next element. The last pointer of the list is a null pointer in order to indicate the end.
We have an extra pointer to the end of the list in practice in order to speed up operations.
Doubly Linked List (Doppelt verkettete Liste)
We also store a pointer to the previous element in a DLL in order to speed up some operations. This increases memory usage as a trade-off for speed.
Runtimes for the operations are identical for SLL and DLLs (except delete)
insertis as we know the memory address of the final element in the list and just have to adjust the pointer. Otherwise it’sgetis very slow as we need to traverse the entire list up toi.insertAfteris possible in assuming we get the memory address of the element to insert after. We just have to adjust the pointer.deletejust adjusts the pointer of the previous element to point to the same location as the pointer of the deleted element did.- In a SLL, this means we have to traverse the entire list up to
i-1to find the previous element: - In a DLL, we know the address of the previous element and can just go edit it’s pointer:
- In a SLL, this means we have to traverse the entire list up to
ADT Stack (Stapel oder Keller)
Similar to list but with more constrained operations which allows more efficient implementation.
Operations
push(k, S): push a new objectkto the top of the stackSpop(S): remove and return the top element of the stackStop(S): get the top element of the stackSwithout deleting it
Other operations might be isEmpty or emptystack which produces an empty one.
The stack can efficiently be implemented by a Singly Linked List. New elements are pushed to the beginning of the list.
pushinserts a new one at the beginning in time.popremoves the first element of the list, so it just rewrites our start pointer to the same address as the pointer of the first element:
ADT Queue (Schlange)
In the ADT Queue we can only access the oldest element and append at the back. This is also called a FIFO (first in first out).
Operations
enqueue(k, S)appends the elementkto the end of the queuedequeue(S)removes and returns the first element of the queue
This can be efficiently implemented using a SLL again, as long as we have a pointer to the last element. We then insert at the end and delete from the front like before, both in .
If we know the maximum size we can use a ringbuffer array which pretends the last element of the array is directly in front of the first (like a ring).
ADT PriorityQueue (Prioritätswarteschlange)
A priority queue stores a natural number which indicates the importance of the element and returns them in the order of that “priority”.
Operations
insert: insert a new object with keykand prioritypintoPextractMax: removes and returns the element with the highest priority.
There are no guarantees in the case of a tie-break, this is implementation dependent.
We can use the MaxHeap to store the data here, which guarantees for both operations.
Some algorithms require operations like remove and increaseKey which are non-trivial.
ADT Dictionary (Wörterbuch)
The ADT Dictionary manages a set of distinct keys (under each key k, data is saved). It implements the following methods:
search(x, W)returns the position of the keyxin memoryinsert(x, W)Insert the keyxintoW, as long as it’s not saved there yetdelete(x, W)find and delete the keyxfromW
The simplest implementations can use unsorted arrays for example. Unfortunately, most operations are then really slow:
| search | insert | delete | |
|---|---|---|---|
| unsorted Array | |||
| sorted Array | |||
| DLL | (you cannot use binary search) |
Binary Search Trees
A binary search tree is a tree with the following search-tree condition: “for every node x in the tree, all keys under the left child are smaller than all the keys x under the right child node.”
This enables search in where is the height of the binary tree (using recursion over the nodes). Inserting and deleting also takes to run.
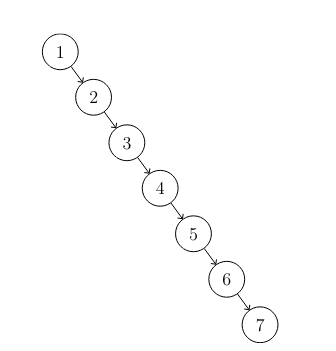
The issue is that binary trees are not balanced by nature, which means that their height can massively overshoot that of . Inserting a list in sorted order produces a tree that looks like this:
Search Algorithm
With this procedure we can find any key in steps at most.
if p is null return "nicht gefunden"
else if p = p.key return p
else if x < p.key return Search(x, p.left) # Smaller so left Subtree
else return Search(x, p.right) # Bigger so in right subtreeInserting
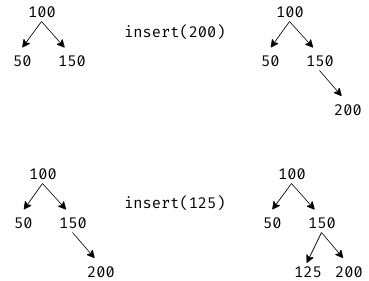
To insert a key into a binary search tree, we:
- search the tree for
- If we find , nothing to do
- Otherwise, we continue until we find a node with no child in the correct direction. We then insert here as a child.
Deleting
We want to delete the key from the tree. We search for it first:
- If has 0 children, we simply remove it
- If has 1 child, we replace by it’s child
- If has 2 children, we replace by the key with the smallest value in it’s right subtree.
- This makes sense because that child will be bigger than all in the left, but smaller than all in the right → the perfect separator.
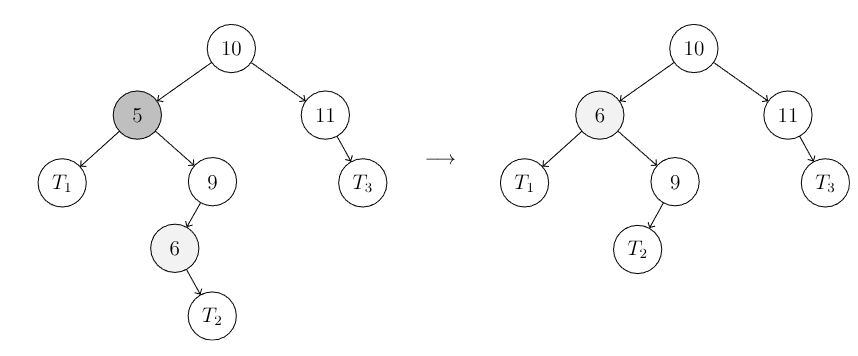
- This makes sense because that child will be bigger than all in the left, but smaller than all in the right → the perfect separator.
2-3 Trees
To fix this issue, we can use “2-3 Trees” which are more flexible. The tree condition here is that each node has 2 or 3 children but that all leafs are on the same level. They will thus be realised as external search-trees in which the keys are only stored in the leaves.
- A node with 2 children has a single separator such that all keys in the left sub-tree are and all in the right are .
- A node with 3 children has two separators such that
- keys in the left sub-tree: all keys
- keys in the middle sub-tree: all keys
- keys in the right sub-tree: all keys
Thus a 2-3 Tree of height has at least leaves. The height of the tree with keys is always limited to so (except for the case ).
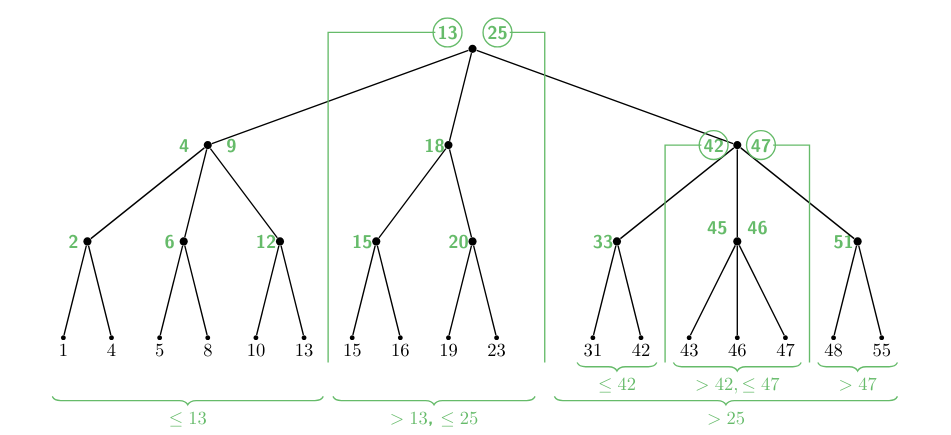
Search
Search can be realised in as the tree is now “balanced”. We simply descend the tree always comparing the searched x with the separators.
Insert
Inserting is done in two steps:
- Search for the correct place in the tree, under which the key will be inserted
- From the script: The value of the key is inserted as a new separator This does not always work however, so you insert one (the middle one’s mostly) of the children’s values as a separator.
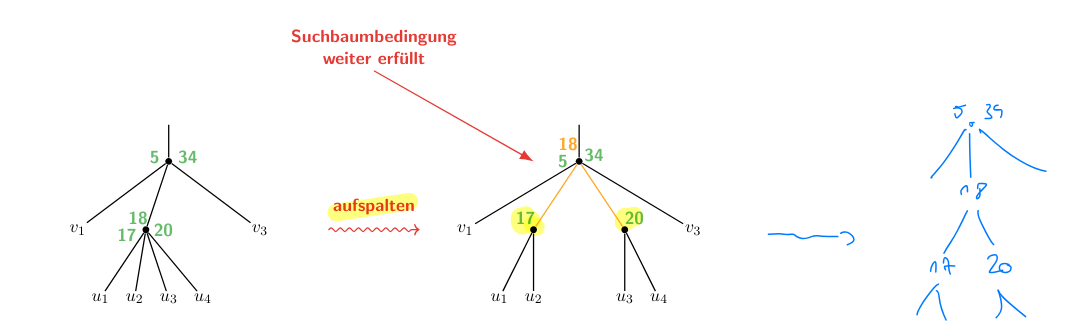
- Rebalance the tree: If the insertion of the new key violates the 2-3 condition, we have to rebalance the tree:
- The node will be split up into two new nodes (each of which get 2 children and one separator)
- The middle of the three separators is pushed to the next higher node
- Here we might have pushed the problem to the next level, thus repeat the balancing there…
Delete
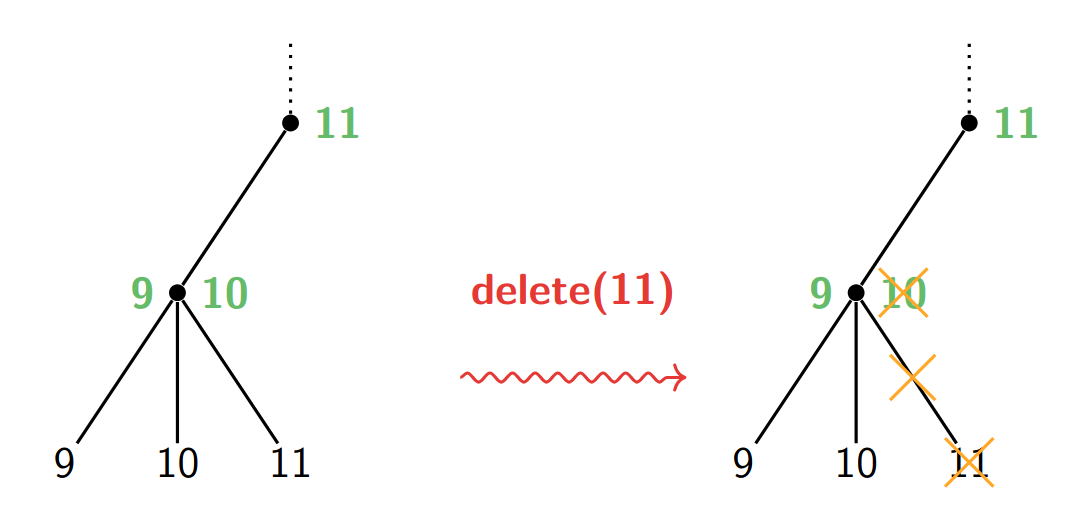
Deletion is slightly done in the same way:
- Search for the key in the tree and remove it. One of the separators will also be removed from the parent node.
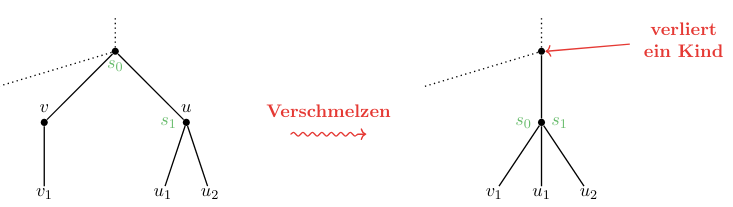
- Rebalance (if necessary): If a neighbouring node has
- 3 children → our current node “adopts” one of the children. The separators have to be updated.
- 2 children → the nodes and are merged to form one new node with 3 children.
- The separator from the parent node is pulled down to be the new .
- This causes the parent to lose a child, thus we might need to rebalance there.
- This can go up to the root. If the root has only a single child, it is removed and the child is the new root.
Runtime of deletion is also bounded by the tree-height and thus takes time.

Summing Up:
| search | insert | delete | |
|---|---|---|---|
| 2-3 Tree |