6. Graphs and closed Eulerian Walks

Eulerian Walks

Conditions for a Eulerian Walk

If there exists a Eulerian walk, then all but at most two vertex degrees must be even.

Only the start and end vertices can have an uneven number of edges. As we start (and end) there, we didn’t mark an edge coming in (going out). Thus they have can have one incident edge more.

The proof idea for this is that every vertex we pass by must have an even number of incident edges, as we come and go the same number of times.

Degree of vertex in a walk

For a walk $W=(v_0,\dots ,v_l)$ we define the degree ${\mathrm{deg}}_W(u)$ of a vertex $u$ to be the number of edges in $W$ incident to $u$ (with repetitions counted) ${\mathrm{deg}}_W(u)=|\{i\in \{0,\dots ,l-1\}|u\in (\{v_i,v_{i+1}\}\}|$

If an edge is used more than once in a walk, then ${\mathrm{deg}}_W(u)$ could be bigger than $\mathrm{deg}(u)$.

Closed Eulerian Walks

A walk is closed if it starts and ends with the same vertex $v_0=v_l$. A path is a walk without repeated vertices.

Closed Walk degree

A walk $W=(v_0,\dots ,v_l)$ is closed if and only if ${\mathrm{deg}}_W(v_l)$ is even.

Each occurence of $v_l$ in the inner part of the walk increases ${\mathrm{deg}}_W(v_l)$ by 2 (in and out) and thus doesn’t affect the parity. Thus ${\mathrm{deg}}_W(v_l)$ can only be even if it occurs once and the start and once at the end at least, i.e. $v_0=v_l$.

Therefore, a closed Eulerian walk is a walk that visits every edge once.

Closed Eulerian Walk conditions in closed graph

A connected graph has a closed Eulerian walk if and only if all vertex degrees are even.

Proof:

• In a closed walk, by our previous theorem all edge degrees are even. If $W$ is Eulerian, then the degrees are the same as in the graph (because we visit each edge only once) $⟹$ ${\mathrm{deg}}_W(u)=\mathrm{deg}(u)$ for all $u\in W$.
• The other direction will need an algorithm that outputs a solution if all vertex degrees are equal. Algorithm to find a Eulerian Path

Even vertex degrees in Eulerian Walk

In a (non-closed) Eulerian Walk, the same holds if we account for the two edges with odd degrees. By adding a new vertex connecting both of them, we make the problems the same. This new edge makes both of their degrees even…

Hamiltonian Path

In comparison to Eularian paths which can be found in $O(n+m)$, Hamiltonian paths can only be found by brute-force search (another $N\ne NP$ problem).

Graph properties

Handshake Lemma

For every graph $G=(V,E)$, ${\sum }_{v\in V}\mathrm{deg}(v)=2|E|$

Proof idea: Suppose every vertex distributes a coin to each of it’s incident edges. Then each edge has two coins one from each endpoint, thus the sum of the vertex degrees is twice the number of edges.

Algorithm to find a closed Eulerian Path

The first step to find a closed Eulerian path is to be able to find closed walks in a connected graph. 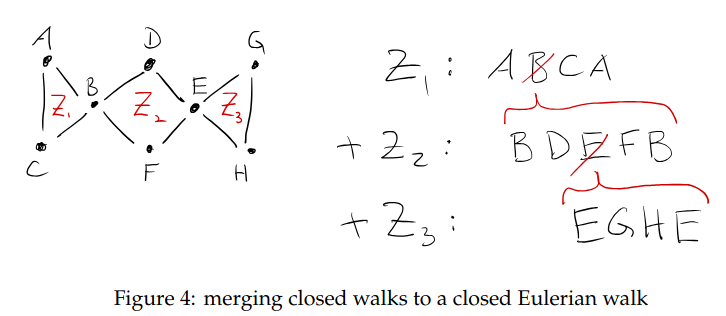If we can find multiple, we can exploit any common edges to merge them together.

We iteratively compute closed walks $Z_1,\dots ,Z_k$ until every edge is used once and then merge them to a closed Eulerian walk.

def walk(u):
	if exists_unmarked_edge(u, v):
		mark(u, v)
		walk(v)

We start at $u$, walking $W$. Every edge gets marked once, as we check before marking. The walk ends in a vertex $v$ such that all incident edges are marked (as we only stop once there are no more incident edges).

We call the walk() function starting with different vertices, never undoing the marking. At the end, we’ll have all closed walks.

We claim that ALL-EVEN “every vertex is incident to an even number of unmarked edges” is an invariant of walk(). Furthermore, the walk $W$ marked by walk(u) is closed.

Proof: If $W$ is closed, then ${\mathrm{deg}}_W(w)$ is even for all vertices $w\in V$, thus ALL-EVEN holds as we only reduced unmarked edges by an even number.

Assume $W$ ends in $v$. Before the walk ALL-EVEN held, and thus $v$ had an even number of unmarked edges. After running walk(u) $v$ now has no unmarked edges, as the walk ends there. Hence ${\mathrm{deg}}_W(v)=0$ is even. Thus walk(u) marked a walk $W$, as all vertices have an even number of edges in the walk.

$⟹$ we can partition the edges of any graph without odd degree vertices into a collection of closed walks by repeatedly running the walk function on vertices with unmarked edges.

We can then merge these together to create one Eulerian walk.

Faster Algorithm

We can use backtracking and recursive functions to make this more efficient. Now, we iterate over all vertices to start our walk routine.

Z = list()
 
def euler_walk(u):
	for edge (u, v) in E incident to u:
		if (u, v) not marked:
			mark(u, v)
			euler_walk(v)
	Z.append(u)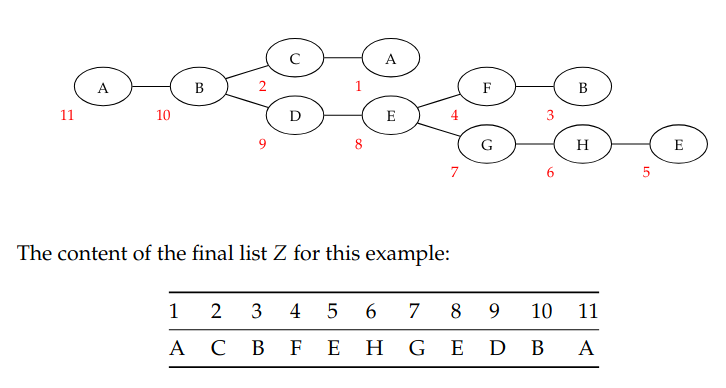

Because we only go back to the last vertex with a still unmarked edge, we can use a single call of euler_walk to find all the closed walks.

def Euler(G):
	Z = list()
	euler_walk(u0 in G) # u0 here is arbitrary
	return Z

Adjacency Matrix Runtime

$G$ is a graph with $n\ge 1$ vertices and $m\ge 1$ edges.

The adjacency matrix $A=(A_{ij}{)}_{i,j\in V}$ of $G$ is defined as $A_{ij}=\{\begin{array}{ll}1& \text{if }\{i,j\}\in E,\\ 0& \text{otherwise}\end{array}$

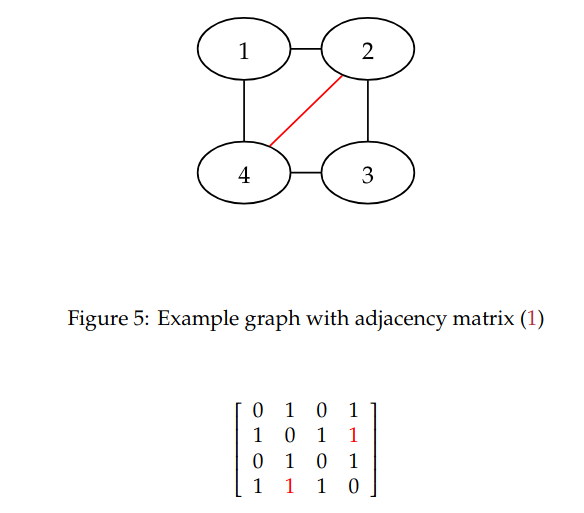
Runtimes:

• Test if for $u,v\in V$, $uv\in E$ is $O(1)$ as it’s simply array lookup.
• Enumerating the neighbors is $\Theta (n)$, as we need to check the entire column/row.

Euler(G) can be implemented in $O(n\cdot m)$ using an adjacency matrix.

• As each recursive call to euler_walk(u) is bounded by $O(n)$ to iterate through the adjacency matrix
• We have a maximum of $m+1$ calls to euler_walk (as there are at most $m$ edges and minimum $1$).

Adjacency List Runtime

An adjacency list represents the graph as a list of vertices, each cell of which contains the indices of the neighbours of that vertex: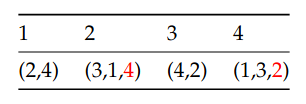

Runtimes:

• We can test for the existence of an edge $uv\in E$ in time $O(1+\min \{\mathrm{deg}(u),\mathrm{deg}(v)\})$
• Given a vertex $u\in V$ we can enumerate the neighbours in time $O(1+\mathrm{deg}(u))$

This data-structure is more suited to our function euler_walk as it’s faster for the enumeration of the neighbours.

Running time to enumerate all edges of $G$ in adjacency list

The runtime to enumerate all edges of $G$ given its adjacency list representation is $O(n+m)$

As enumerating the neighbours of a single vertex takes time $O(1+\mathrm{deg}(u))$, the total runtime is: $O({\sum }_{u\in V}(1+\mathrm{deg}(u)))$ And using the handshake lemma, that comes out to $su{m}_{u\in V}(1+\mathrm{deg}(u))=n+{\sum }_{u\in V}\mathrm{deg}(u)=n+2m$

Without the $+1$ term, we might have been tempted to conclude $O(m)$, but for graphs with way more vertices than edges that is false.

As each euler_walk takes $O(1)$ (plus the $O(1)$ ops carried out in euler_walk(u0)), we can say that it runs in $O(m+1)$. The initialisation of the adjacency matrix takes $O(n+m)$.

Thus the total runtime is $O(n+m)$.

Correctness

Euler(G) computes a closed Eulerian Walk

For a connected graph $G$ without odd degree vertices, Euler(G) computes a closed Eulerian walk.

Proof: To prove this we will use the recursion tree $T$ of the euler_walks and the tortoise and the hare analogy.

We note that each edge of $G$ is represented precisely by one edge in $T$. Since euler_walk traverses an edge only if it hasn’t been travelled before, each edge appears only once in $T$. As $G$ is connected, it also appears at least once in $T$. Thus each edge is exactly once in $T$.

The hare walks from the root to the first leaf, then back up to the first intersection and down to the second leaf, until it walks from the last leaf to the root again. Then it has traversed every edge of $T$ exactly twice. The tortoise waits at the first leaf for the hare, then walks up to the first intersection and jumps immediately to the second leaf, until it’s at the last leaf then to the root. Thus it walks every edge exactly once, and has thus completed a Eulerian walk.

Cycle Detection

If a non-repeating walk exists (i.e. an Eulerian Path), then that walk must be a cycle. If a cycle exists, we are guaranteed to find it with our algorithm.

Remarks from the Exercise Sheet 8

Cut Vertex

If a vertex of degree $\ge 2$ is not a cut vertex, then it must lie on a cycle.

Remarks from the Exercise Sheet 9

Bipartite Grpah

A graph is bipartite if and only if it does not contain any cycles of odd length.