7. Topologische Sortierung (DFS)

We work with directed Graphs here, which means that the edges $e$ are ordered pairs instead of sets here, i.e. $e=(u,v)$ ($u$ ist der Vorgänger von $v$, $v$ der Nachfolger von $u$), which means that the edge has a direction, we can travel in, while the other is not allowed.

We define the:

• In-Degree ${\mathrm{deg}}_{in}(u)$ as the number of edges directed into the vertex $u$.
• Out-Degree ${\mathrm{deg}}_{out}(u)$ as the number of edges directed out of vertex $u$.

There are special vertices in directed graphs:

• Source (de: Quelle): a vertex $u$ with ${\mathrm{deg}}_{in}(u)=0$ is called a source.
• Sink (de: Senke): a vertex $u$ with ${\mathrm{deg}}_{out}(u)=0$ is called a sink.

To represent a directed graph, we can use the same adjacency list or adjacency graph as previously, only that we have a $1$ in $M_{uv}$ if $e=(u,v)$ exists but not in $M_{vu}$.

Topological Ordering

In a directed graph, a topological ordering is a linear ordering of the vertices such that for every directed edge $(u,v)$, vertex $u$ comes before vertex $v$ in the ordering. This means that all arrows point rightwards.

Not all graphs have such a topological ordering. The existence of a directed cycle prevents this, as then there is no vertex that comes “first”.

Existence of a topological ordering

There exists a topological ordering $\iff$ There does not exist a directed Closed Walk.

A directed graph has a topological ordering if and only if it’s a Directed Acyclic Graph (DAG), meaning it contains no cycles.

Topological Sort Algorithm

The core idea of the topo-sort algorithm is that it repeatedly finds and locates sinks and removes them from the graph. We can then put the sink $v$ at the last place in our list, remove it and solve the rest recursively.

Visit function

We define the visit function:

def visit(u, topological_order):
   u.mark()
   for v in u.successors():
   	if not v.isMarked():
   		visit(v, topological_order)
   topological_order.insert(0, u)   # Prepend u to maintain order

Visit processes all vertices reachable from $u$ before adding $u$ to the order, meaning that all vertices depending on $u$ come first. This is what we require for topo-sort.

To show that this approach works, we need to prove the following:

If there is no closed walk, a sink exists

If there is no closed walk (Zyklus) in $G$ $⟹$ exists a Sink

Proof There is a path $P$ ending in $v$, found by our path algorithm - this means that $v$ has no more unmarked successors. If we assume for contradiction that $v$ is not a sink, then there exists a marked successor $w$, which means there is a cycle - contradiction.

DFS (Depth First Search)

We have the following function that performs DFS and finds a topological ordering:

def dfs_topological_sort(G):
	G.unmarkAll()
	topological_order = []
	for u in G.nodes():
		if not u.isMarked():
			visit(u, topological_order)
	return topological_order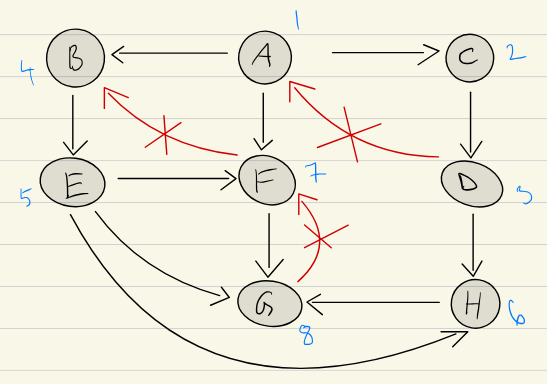

has the following recursion tree when we run DFS on it.

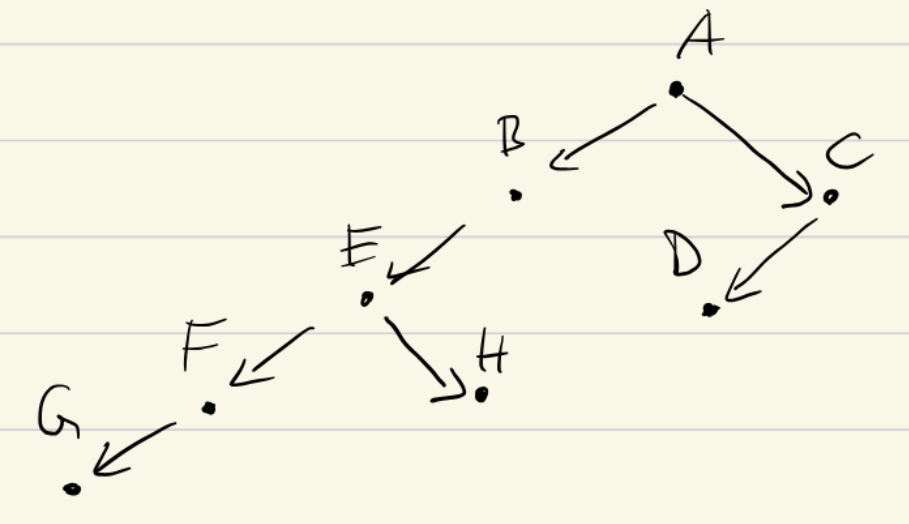
Deeper understanding using pre- and postordering

We can augment the DFS implementation by also tracking in what order which edges and vertices were visited:

def visit(u, topological_order, pre, post, T):
    pre[u] = T
    T += 1
    u.mark()
    for v in u.successors():
        if not v.isMarked():
            T = visit(v, topological_order, pre, post, T) # T is modified recursively.
    topological_order.insert(0, u)
    post[u] = T
    T += 1
    return T

Note: DFS can be implemented efficiently using a stack, similar to how BFS uses a queue.

This gives us the following Graph:

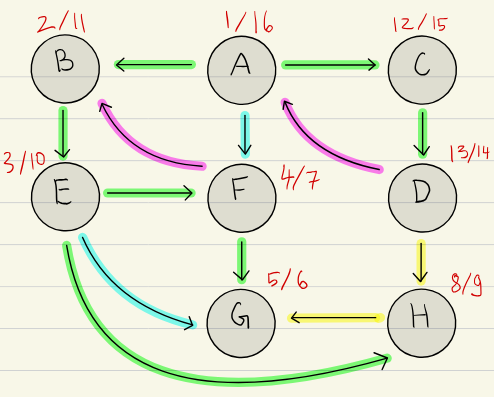
We can then define an Intervall $I_u=\{\text{pre}[u],\dots ,\text{post}[u]\}$. We then have a nesting of the different intervals, which is a different way to draw the recursion tree:

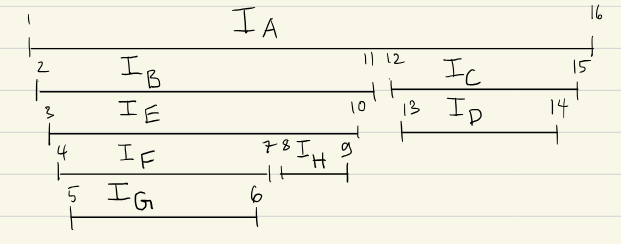
We can then classify the edges based on the interval patterns of the connected vertices:

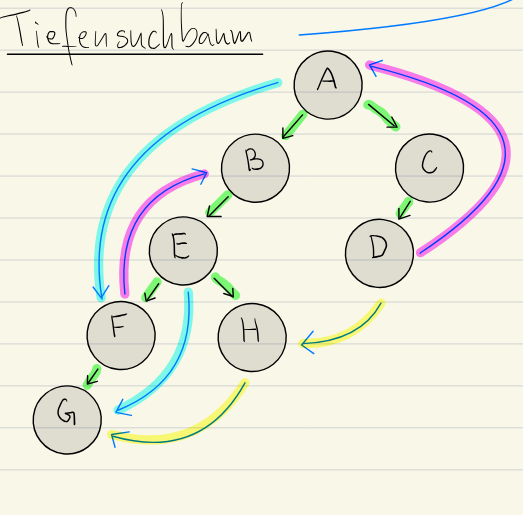
DFS Edge Classification

1. Tree Edge: If $\text{pre}(u)<\text{pre}(v)<\text{post}(v)<\text{post}(u)$, then $(u,v)$ is a tree edge. This means $v$ is a descendant of $u$ in the DFS tree. The visit(u) call directly leads to the visit(v) call.
   *Example: $(A,B)$, $(B,E)$

2. Back Edge: If $\text{pre}(v)<\text{pre}(u)<\text{post}(u)<\text{post}(v)$, then $(u,v)$ is a back edge. This indicates a cycle in the graph. $u$ is a descendant of $v$, and the edge $(u,v)$ goes back to an ancestor.
   *Examples: $(F,B)$, $(D,A)$

3. Forward Edge: If $\text{pre}(u)<\text{pre}(v)<\text{post}(v)<\text{post}(u)$, then $(u,v)$ is a forward edge. This means $v$ is a descendant of $u$, but the edge is not part of the DFS tree. There is a path from $u$ to $v$ in the tree but a direct edge as well.
   Examples: $(A,F)$, $(B,G)$

4. Cross Edge: If $\text{pre}(v)<\text{post}(v)<\text{pre}(u)<\text{post}(u)$, then $(u,v)$ is a cross edge. This means $u$ and $v$ are in different branches of the DFS tree, and there is no ancestor-descendant relationship between them. They belong to different subtrees that don’t overlap.
   Examples: $(H,G)$, $(D,H)$

Impossible Cases:

• Overlapping but not Nested Intervals:
  • Due to the recursive nature of DFS, two intervals cannot partially overlap without one completely containing the other.
• $\text{pre}(u)<\text{pre}(v)<\text{post}(u)<\text{post}(v)$:
  • This case is impossible because visit(u) would call visit(v) if v was not yet marked, so the interval of v can’t end before u.

Observations

(1)

$\exists$ back-edge $⟹$ $\exists$ directed closed walk

(2)

$\forall$ not back-edge $(u,v)\in E$, $\text{post}(u)\ge \text{post}(v)$

We can conclude from this that if $\nexists$ directed closed walk $\stackrel{(1)}{⟹}$ that $\nexists$ back-edge $\stackrel{(2)}{⟹}$ reversed post-order (our DFS output) is topological sorting.

Topological Sorting from Post-Order

The reversed post-order is a topological order.

DFS in undirected Graphs

In an undirected Graphs, we have two more properties that hold:

1. back-edges = forward-edges
2. cross edges are not possible

Find cycles using DFS

If during the execution of DFS, we add the additional check of checking all adjacent nodes, we can detect cycles.

If we find an adjacent vertex without a post-number, this means there’s a back-edge. If we find one with both pre- and post-number, there’s a cross-edge.

Bipartite Check with DFS

Same as with BFS, maintain a colouring of all vertices. If during traversal, there’s an edge to a vertex with the same colour, there’s an odd cycle and we return false.

Runtime Analysis of Topological Sorting

Adjacency Matrix

• visit is called $n$ times (one call per vertex)
• visit(u) takes $O(n)$ + time in recursive calls Total: $n\cdot O(n)=O(n^2)$Thus DFS has a runtime of $O(n^2)$ with the adjacency list.

Adjacency List

• visit(u) takes $O(1+{\mathrm{deg}}_{\text{out}}(u))$ + time in recursive calls Total: ${\sum }_{u\in V}(1+{\mathrm{deg}}_{\text{out}})=|V|+{\sum }_{u\in V}{\mathrm{deg}}_{\text{out}}(u)$Thus DFS has a runtime of $O(|V|+|E|)$ with the adjacency list.

This means that in sparse graphs the adjacency list performs better, while in densely connected graphs where $m\approx n^2$, we have a better performance with the adjacency matrix.

Specifically, if $|E|\ge |V{|}^2/10$, then DFS has the same runtime in the worst-case using adjacency matrices or lists.