1. Vectors

1.1 Vectors and linear combinations

The subtraction of one vector $v_2$ from $v_1$, $v_1-v_2$ is the vector going from the tip of $v_2$ to the tip of $v_1$.

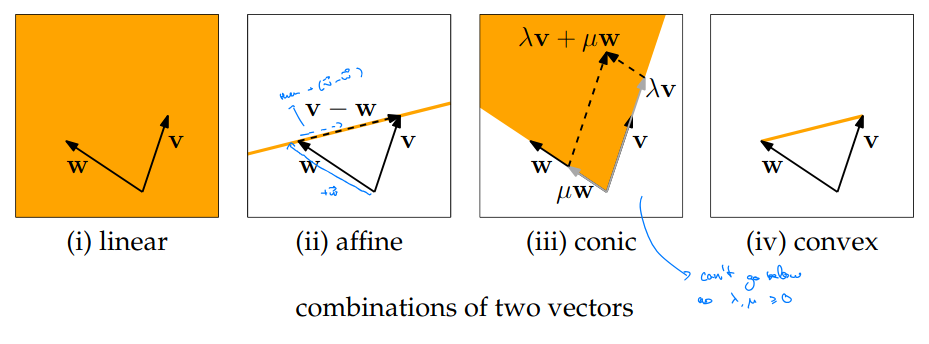
1.1.4 Affine, conic and convex combinations

1.7 Affine, conic, convex combination

A linear combination of vectors is called

• an affine combination if ${\lambda }_1+{\lambda }_2+\cdots +{\lambda }_n=1$
• a conic combination if ${\lambda }_j\ge 0$ for $j=1,2,\dots ,n$
• a convex combination if it is both affine and conic

1.2 Scalar products, lengths and angles

1.2.1 Scalar Product

The scalar product is defined as: $v\cdot w={\Sigma }_{i=1}^n{v}_i{w}_i$

1.9 Scalar Product Properties

$u,v,w\in {\mathbb{R}}^m$ be vectors and $\lambda \in \mathbb{R}$ a scalar:

• $v\cdot w=w\cdot v$ (symmetry / commutatitivity)
• $(\lambda v)\cdot w=\lambda (v\cdot w)$ (scalars move freely)
• $u(v+w)=u\cdot v+u\cdot w$ and $(u+v)w=u\cdot w+u\cdot v$ (distributivity)
• $v\cdot v\ge 0$ with equality exactly if $v=0$ (positive definiteness)

The scalar product measures “how much the vectors point in the same direction”. It projects the length of one onto the other and then multiplies those lengths. The more they are aligned, the longer this projection will be.

Note that if $v$ and $w$ are orthogonal, we have $v\cdot w=0$ which holds because: $v\cdot w=||v||||w||\cdot \cos \alpha$ and $\cos \alpha =0$ if $\alpha =90$. From this definition we can also see that $\text{0}$ is orthogonal to all vectors.

1.2.2 Euclidean Norm

1.11 Euclidean norm

The euclidean norm of $v$ is the number $||v||:=\sqrt{v\cdot v}$

This means that $v^{\top }v=||v|{|}^2$.

Unit vector

A unit vector is a vector such that $||v||=1$.

We can produce unit vectors by dividing by the vector’s norm: $v^{\prime }=\frac{v}{||v||}$.

1.2.3 Cauchy-Schwarz Inequality

Cauchy-Schwarz Inequality

$|u\cdot w|\le ||u||||w||$ It holds exactly if and only if $\exists \lambda \text{s.t.}u=\lambda w$ (scalar multiple of each other).

1.2.4 Angles

Angle between vectors

$\cos \alpha =\frac{v\cdot w}{||v||||w||}$

1.15 Orthogonal Vectors

Two vectors $v,w\in {\mathbb{R}}^m$ are orthogonal if $v\cdot w=0$. In other words if the cosine of the angle between them is $0$ and the angle thus $90$ degrees.

As the scalar product of $0$ with any vector is $0$, all vectors are orthogonal to $0$.

1.15 Hyperplane through the origin

A hyperplane is defined as the set of all orthogonal vectors to a $v\in {\mathbb{R}}^m,v\ne 0$. $H_d=\{\text{v}\in {\mathbb{R}}^m:\text{v}\cdot \text{d}=0\}$

Hyperplane dimension

A hyperplane $H$ through the origin of ${\mathbb{R}}^m$ has dimension $m-1$ (Assignment 6).

1.2.5 Triangle Inequality

Triangle Inequality

$||v||+||w||\ge ||v+w||$ It holds exactly if $\exists \lambda \text{s.t.}u=\lambda w$.

1.2.6 Covectors and $v^{\top }w$

The scalar product can also be written as ${\text{v}}^{\mathsf{T}}\text{w}$. The transpose ${\text{v}}^{\mathsf{T}}$ is a covector, written as a row vector instead of a column vector.

Formally a covector is a function ${\text{v}}^{\mathsf{T}}:x⟼{\sum }_{i=1}^m{v}_i{x}_i$.

1.3 Linear (in)dependence

Introduction

If $\exists \lambda \in \mathbb{R}$ such that $u=\lambda v$ then $u$ and $v$ are colinear. This means that they are on the same line.

Two vectors in ${\mathbb{R}}^3$ cannot span the whole space, but they automatically form a plane (except if they are colinear).

To check if three vectors are coplanar, you have to check if $\exists \lambda ,\mu \in \mathbb{R}$ such that $\lambda v+\mu u=w$.

1.3.1 Definitions and Examples

Dependance:

• At least one vector in the set is a linear combination of the other ones.
• $0$ is a non-trivial combination of the vectors in the set (this means that there is a linear combination in which at least one ${\lambda }_i\ne 0$).
• At least one of the vectors is a linear combination of the previous ones.

Independance:

• None of the vectors is a linear combination of the other ones.
• There are no ${\lambda }_i$ besides all $0$ such that the linear combination sums to $0$ (i.e. there is only the trivial combination).
• None of the vectors is a linear combination of the previous ones.

IMPORTANT

For each $u\in C(A)$, there is a unique set of ${\lambda }_1,\dots ,{\lambda }_n$ such that ${\lambda }_1{v}_1+\cdots +{\lambda }_n{v}_n=u$ A linear combination of linearly independent vectors can only be written in one way.

Edge Cases:

1. Any sequence of vectors which contains the $\text{0}$ vector is linearly dependant by definition. Set all other $\lambda$‘s to 0 and the scalar factor of the zero vector to $\forall \lambda \in \mathbb{R}$.
2. Any sequence of vectors which contains a vector twice is dependent, since you can set their $\lambda$‘s to be opposite.
3. The empty set is always linearly independent (since there is no vector $v_k$ to compare).

1.3.3 Span of Vectors

1.25 Span

The span of a set of vectors is the set of all linear combinations:$\text{Span}({\text{v}}_1,{\text{v}}_2,...,{\text{v}}_n):=\{{\sum }_{j=1}^n{\lambda }_j{\text{v}}_j:{\lambda }_j\in \mathbb{R}\text{for all}j=[n]\}$

Example: in ${\mathbb{R}}^3$ there are three possible cases:

• a line through the origin
• a plane
• the entire space

Zero always in span

$\text{0}\in \text{Span}$ for any vectors, even if it’s the empty set ($\text{Span}()=\{\text{0}\}$).

1.26 Linear combination doesn't change the span

Adding or removing an element from the set doesn’t change the span if the element is a linear combination of the other vectors.

1.28 Span the space

The span of $m$ linearly independent vectors is ${\mathbb{R}}^m$.