2. Matrices

2.1 Matrices and linear combinations

2.2 Matrix Properties

• The addition of two matrices happens element-wise.
• The scalar multiplication of a matrix is also element-wise.
• The zero matrix is the matrix in which every element is 0.
• If m (rows) = n (columns) the matrix is square.

Here are a few special matrix forms:

2.3 Kronecker delta

The Kronecker delta is a function taking in $i,j$ and outputting $1$ if $i=j$ else $0$. It’s used to define the Identity matrix.

2.3 Identity Matrix

The identity Matrix $\text{I}$ is defined as $\text{I}:=[{\delta }_{ij}{]}_{i=1,j=1}^{mm}$

Extra: Nilpotency

Nilpotent

A matrix $A$ is called nilpotent if there exists a $k\in \mathbb{N}$ such that $A^k=0$.

Such a matrix $A$ does not have an inverse.

2.1.1 Matrix-Vector multiplication

$A\text{x}$ is the multiplication of Matrix $A\in {\mathbb{R}}^{m\times n}$ with the vector $\text{v}\in {\mathbb{R}}^n$

• The result is a vector with $m$ rows: each row is the scalar product of row $a_i$ with $x$.
• The resulting vector is the sum of all columns $a_j\times x_i$ → this is the definition of the linear combination. The matrix-scalar multiplication is thus basically a linear combination.

2.5 Linear combinations and independence

1. A vector $b\in {\mathbb{R}}^m$ is a linear combination of the columns of $A$ if and only if there exists a vector $x\in {\mathbb{R}}^n$ (of suitable scalars) such that $Ax=b$
2. The columns of $A$ are linearly independent if and only if $x=0$ is the only vector such that $x=0$.

2.7 Identity Matrix

The Identity matrix times a vector gives back that exact vector: $\forall v\in {\mathbb{R}}^{m}Iv=v$

Note that matrix-vector multiplication can be viewed from two perspectives:

1. Column View: When doing $Ax$, $x$ contains the coefficients by which we multiply each of the columns of $A$, giving us a linear combination.
2. Row View: Each entry of $b$ in $Ax=b$ is the linear combination of a row of $A$ and $x$: $b_1=u_1^{\top }x$

2.1.2 Column space and rank

2.9 Column space

The column space of a matrix $\text{C}(A)$ of $A$ is the span (set of all linear combinations) of the columns (interpreted as vectors): $\text{C}(A):=\{Ax:x\in {\mathbb{R}}^n\}\subseteq {\mathbb{R}}^m$

Note that in the same way as $\text{0}$ is always in the span of any set of vectors, $0$ is always part of the column space.

2.10 Rank

The rank of a matrix $\text{rank}(A)$ $A\in {\mathbb{R}}^{m\times n}$ is a number between $0$ and $n$ which counts the number of independent columns. A column is independent if it is not the linear combination of the previous ones (or the next ones, if you do it the other way round).

0 Rank

The rank is $0$ exactly if $A$ is the zero matrix.

Note that we can reorder the columns of a matrix and thus get different independent columns, but the rank will stay the same.

2.11 Independent Columns span the column space

The independent columns of $A$ span the column space $\text{C}(A)$ of $A$.

This can be proven by lemma 1.26 (adding elements that are a linear combination of the other ones, doesn’t change the span).

2.1.3 Row space and transpose

We can also define the row-space as the space spanned by the rows and the row-rank as the number of independent rows.

Row-rank = Column-Rank

The rank of the rows and the columns is always the same!

2.12 Tranpose

The transpose of $A$ is the matrix $A^{\top }$ where $A_{ij}=A_{ji}^{\top }$.

2.13 Transposing twice

For all matrices $A$: $(A^{\top }{)}^{\top }=A$

2.13 Symmetric

A matrix $A$ that is square is symmetric if and only if $A^{\top }=A$.

2.14 Row space

$\text{R}(A):=\text{C}(A^{\top })$

2.1.5 Nullspace

2.17 Nullspace

Let $A$ be an $m\times n$ matrix. The nullspace of $A$ is the set $\text{N}(A)=\{x\in {\mathbb{R}}^n:Ax=0\}\subseteq {\mathbb{R}}^n$

Note that the $0$ vector is always in $\text{N}(A)$.

2.2 Matrices and linear transformations

2.18 Matrix Transformation

$T_A:{\mathbb{R}}^n\to {\mathbb{R}}^n$ is the function where $x\in {\mathbb{R}}^n$ and $Ax\in {\mathbb{R}}^m$ defined by: $T_A(x)=Ax$

2.19 Linearity Axioms

Let $A$ be an $n\times m$ matrix, $x_1,x_2\in {\mathbb{R}}^n$ and ${\lambda }_1,{\lambda }_2\in \mathbb{R}$. Then $A({\lambda }_1{x}_1+{\lambda }_2{x}_2)={\lambda }_{1}A{x}_1+{\lambda }_{2}A{x}_2$

Because we can express every vector $x\in {\mathbb{R}}^n$ as the linear combination of the unit vectors $e_1,\dots ,e_n$, we can reconstruct what happens to every single vector by understanding what happens to the unit vectors (thanks to linearity).

2.2.2 Linear Transformations and linear functionals

2.21 Linear Transformation

A function $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ / $T:{\mathbb{R}}^n\to \mathbb{R}$ is called a linear transformation / linear functional if the following linearity axiom holds for all $x_1,x_2\in {\mathbb{R}}^n$ and all ${\lambda }_1,{\lambda }_2\in \mathbb{R}$: $T({\lambda }_1{x}_1+{\lambda }_2{x}_2)={\lambda }_{1}T(x_1)+{\lambda }_{2}T(x_2)$

By this definition, we can deduce that the transformation of a linear combination is the linear combination of the transformed vectors $T({\sum }_{j=1}^l{\lambda }_j{x}_j)={\sum }_{j=1}^l{\lambda }_{j}T(x_j)$

Linear is matrix

Every matrix transformation is a linear transformation.

From definition 2.21 follow the two linearity axioms “light”:

• $T(x+x^{\prime })=T(x)+T(x^{\prime })$
• $T(\lambda x)=\lambda T(x)$ use these to prove that something is a linear transformation as it’s easier to check them in isolation.

2.24 0 maps to 0

For every linear transformation / linear functional we have: $$ T(0) = 0 $$$0$isalwaysmappedtoby$0$!

2.2.3 The matrix of a linear transformation

2.26 Every linear transformation is uniquely described by a matrix

Let $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ be a linear transformation. There is a unique $m\times n$ matrix $A$ such that $T=T_A$ meaning that $T(x)=T_A(x)=Ax$ for all $x\in {\mathbb{R}}^n$.

We can find this matrix using the formula $A=\left[\begin{array}{cccc}|& |& & |\\ T(e_1)& T(e_2)& \dots & T(e_n)\\ |& |& & |\end{array}\right]$

Note that for two matrices $A$ and $B$, $T_A\circ T_B=T_{AB}$.

2.2.4 Kernel and Image

The kernel is the nullspace of a linear transformation. The image is the column space of the linear transformation.

Note that for $T$ linear transformation and the unique matrix $A$ representing it, we have $\text{Im}(T)=\text{C}(A)$ and $\text{Ker}(T)=\text{N}(A)$.

2.3 Matrix Multiplication

2.40 Transpose of multiplication

$(AB{)}^{\top }=B^{\top }{A}^{\top }$ for two matrices with corresponding dimensions.

Note that $IA=A$ and $AI=A$ for all matrices $A$.

2.42 Matrix Multiplication Properties

1. $A(B+C)=AB+AC$ and $(A+B)C=AC+BC$ (distributivity)
2. $(AB)C=A(BC)$ (associativity)

Note that matrix multiplication is not commutative.

2.3.4 Everything is Matrix-Matrix

You can see all types of vector-matrix, matrix-vector, vector-vector, scalar product multiplication as a matrix-matrix multiplication.

We can use associativity to our advantage: If we have a product that has very big intermediate matrices, we can use associativity to simplify it: this means that $w^{⊺}(v{w}^{⊺})v=(w^{⊺}v)(w^{⊺}v)$.

2.3.5 CR Decomposition

CR decomposition

A matrix $A\in {\mathbb{R}}^{m\times n}$ of rank $r$ can be written as the matrix-matrix product $A=C{R}^{\prime }$ where $C$ is the $m\times r$ submatrix containing the independent columns and the unique $R^{\prime }\in {\mathbb{R}}^{r\times n}$ matrix.

You can see why this works intuitively. The result of the multiplication is a matrix in $m\times n$. Each column of $R^{\prime }$ represents the number of times we take each independent column to get the dependent ones.

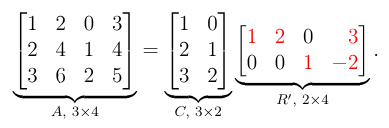
You can see that in the columns of the independent vectors, $R^{\prime }$ is such that the linear combination only contains the vector itself, once. The dependant columns are a combination of the independent ones (see column 2 being 2 times column 1, thus $R^{\prime }$ having (2, 0) as it’s second column.

Note that the C in CR’ decomposition does not need to be a column vector, it can have any width, depending on how many independent columns A has.

Note that by Lemma 1.24 $R^{\prime }$ is unique as there is only one way to write a vector as the linear combination of independent ones.

We can also use CR decomposition to compress a matrix, as the decomposition uses only $(m+n)\cdot r$ entries.

2.4 Invertible and Inverse Matrices

By applying the inverse matrix, you can undo any matrix transformations, as long as this matrix $A^{-1}$ exists.

If the matrix $A$ in $T_A$ is not square, the transformation is not bijective and thus not reversible.

Wide Matrix transformations are not injective

Let $T_A:{\mathbb{R}}^n\to {\mathbb{R}}^m$ be a matrix transformation and $m<n$. Then $T_A$ is not injective. This holds because a transformation from more dimensions into less loses information, so two inputs map to the same output (by the pigeonhole principle).

Tall Matrix transformations are not injective

Let $T_A:{\mathbb{R}}^n\to {\mathbb{R}}^m$ be a matrix transformation and $m>n$. Then $T_A$ is not surjective. This holds because a transformation from less dimensions into more doesn’t map to all outputs, so you can’t reverse all of them.

Now let’s look at inversible, square-matrix linear transformations.

The inverse of a bijective linear transformation is also a linear transformation

Let $T_A:{\mathbb{R}}^n\to {\mathbb{R}}^m$ be a bijective linear matrix transformation. Then $T^{-1}$ is also a linear transformation.

There are three equivalent statements about matrix transformations:

2.53 Equivalences

• (i) $T_A:{\mathbb{R}}^m\to {\mathbb{R}}^m$ is bijective.
• (ii) There is an $m\times m$ matrix B such that $BA=I$.
• (iii) The columns of $A$ are linearly independant.

The third one can be derived from the fact that if $BA=I$, there is only a single $x\in {\mathbb{R}}^m$ such that $A\text{x}=0$. It is also intuitively clear that if not all columns where linearly independent, we’d actually have a tall linear transformation and would be losing information.

Invertible and singular matrix

Let $A\in {\mathbb{R}}^{m\times m}$. $A$ is invertible if there is a $m\times m$ matrix $B$ such that $BA=I$ (only works if $A$ has linearly independent columns). Otherwise, $A$ is called singular.

$A$ is invertible iff (the following equivalent conditions are true):

• $AB=I$
• $BA=I$
• $AB=BA=I$

2.57 Inverse Matrix

The inverse matrix is unique and can be denoted $A^{-1}$.

2.58 Inverse of the Inverse

$(A^{-1}{)}^{-1}=A$

2.59 Inverse of Multiplication

$A$, $B$ invertible matrices $m\times m$. Then $AB$ is also invertible and $(AB{)}^{-1}=B^{-1}{A}^{-1}$

2.6 Inverse of transpose

Let $A$ be an $m\times m$ invertible matrix. Then the transpose $A^T$ is also invertible and: $(A^T{)}^{-1}=(A^{-1}{)}^T$