3. Solving Linear Equations

3.2 Gauss Elimination

Gauss Elimination is Gauss-Jordan without the multiplication.

Row Exchanges

Even after using row-exchanges, the solutions are the exact same. We don’t need to swap around the entries of our solutions.

3.2.3 Row Operations

3.2 Row Operations don't change solutions

Let $A$ be an $m\times n$ matrix and $M$ an invertible $m\times m$ matrix. Then the two systems $Ax=b$ and $MAx=Mb$ have the same solutions $x$.

This justifies why we can use Gauss-Elimination with back-substitution to find solutions to our original LSE. Even though our matrix changes, we only change it in ways that preserve the original solution space.

3.3 & 3.4 Invariance of Independence and Rowspace and Nullspace

For $A$ a matrix and $M$ an invertible matrix:

1. $\text{N}(A)=\text{N}(MA)$ (nullspace is the same)
2. $\text{R}(A)=\text{R}(MA)$ (rowspace is the same)
3. $A$ has linearly independent columns if and only if $MA$ has linearly independent columns.

Note that the column space (and thus also $N(A^{\top })$) is not preserved: $C(A)\ne C(R)$. The rowspace is the same because we take linear operations on the rows (we add/substract) them.

Subspace	Preserved?
$R(A)$	✓
$N(A)$	✓
$C(A)$	✗
$N(A^{\top })$	✗

Example $\left[\begin{array}{cc}1& 2\\ 2& 4\end{array}\right]$ after RREF is $\left[\begin{array}{cc}1& 2\\ 0& 0\end{array}\right]$ which spans a completely different line.

$A$ and $MA$ do however have:

• the independent columns at the same indices
• thus the same rank

3.2.4 Success and failure

3.8 Success of Gauss-Elimination

Let $Ax=b$ a system of $m$ linear equations in $m$ variables. If $A$ has linearly independent columns, then Gauss elimination succeeds and back-substitution finds the unique solution. If $A$ has linearly dependent columns, Gauss elimination fails.

3.2.5 Runtime

Runtimes:

• Gauss Elimination: $O(m^3)$
• Back Substitution: $O(m^2)$ Gauss Elimination with Back-sub: $O(m^2)$ Computing the inverse: $O(m^3)$

3.3 Gauss-Jordan Elimination

G-J elimination works in the general case.

3.3.1 Reduced Row Echelon Form

3.13 RREF

$R$ is in $RREF$ if $\exists r\in \mathbb{N}$:

1. For every $i\in [r]$, column $j_i$ of $R$ is the standard unit vector $e_i$
2. All entries $r_{ij}$ “below the staircase” are $0$.

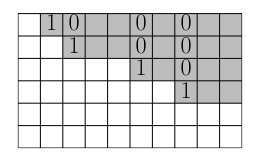
3.14 Independent columns of RREF

A matrix $R$ in $\text{RREF}(j_1,j_2,\dots ,j_r)$ has independent columns $j_1,j_2,\dots ,j_r$ and therefore rank $r$.

Here the $j_1,j_2,\dots ,j_r$ are the indices of the independent columns. Example: The identity matrix is in $\text{RREF}(1,2,\dots ,m)$.

3.3.2 Direct Solution

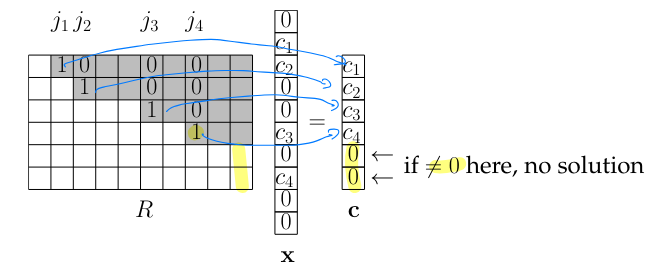
3.3.3 Elimination

We proceed as in Gauss elimination using row operations to transform $Ax=b$ into $Rx=c$ with the same solutions where $R$ in RREF form.

In contrast to Gauss elimination, we can use row division.

Runtime is $O(m^2(m+n))$

3.3.4 Standard Form and CR decomposition

3.17 Output of G-J elimination

Let $A$ be an $m\times n$ matrix and let $(R,j_1,j_2,\dots ,j_r,M)$ be the output of G-J with input $(A,I)$ where $I$ is the $m\times m$ identity matrix. Then $M$ is invertible, $R=MA$ and $R$ is in $\text{RREF}(j_1,j_2,\dots ,j_r)$.

Warning! When we want to find the inverse of $A$, we cannot use row exchanges, as we otherwise get a different $M$.

3.18 Uniqueness and CR

The unique matrix resulting from G-J on $A$ has the following properties

• $R=MA$ for some invertible $M$
• $R$ is in RREF

Technique: Find CR from RREF:

For $R$ result of RREF on $A$, $R$ in $\text{RREF}(j_1,j_2,\dots ,j_r)$ where $R=\left[\begin{array}{c}{R}^{\prime }\in r\times n\\ 0\in (m-r)\times n\end{array}\right]$.

1. This $R^{\prime }$ is the $R^{\prime }$ from the CR decomposition (non-zero rows).
2. And $C$ is the submatrix taking only $j_1,j_2,\dots ,j_r$ (independent columns).

3.3.5 Computing inverse matrices

3.19 Finding the inverse of $A$

To find the inverse of a matrix, we can use G-J on $(A,I)$ and then get $(R,M)$. If $A$ is invertible, $R=I$ and since $R=MA$, $M$ is the inverse of $A$.

Note that $A$ is invertible if and only if $R=I$ in this case (by theorem 3.19).

3.3.6 Solving $Ax=b$

We can then solve an $Ax=b$ using RREF on $(A,b)$ and solving the equations using back substitution.