4. Subspaces

4.1 Vector Spaces

4.1.1 Definition and Examples

4.1 Vector Space

A vector space is a triple $(V,+,\cdot )$ where $V$ is a set (the vectors) and $+$ and $\cdot$ are functions (scalar addition and multiplication). They satisfy the following axioms:

1. $v+w$ = $w+v$ (commutativity)
2. $u+(v+w)=(u+v)+w)$ (associativity)
3. $0$ vector such that $v+0=v$ for all $v$
4. $-v$ for all $v$ such that $v+(-v)=0$
5. $1\cdot v=v$
6. $(\lambda \cdot \mu )v=\lambda \cdot (\mu \cdot v)$
7. $\lambda (v+w)=\lambda v+\lambda w$
8. $(\lambda +\mu )v=\lambda v+\mu v$

Note that: there is

• $0v=0$ for all $v$
• only one $0$
• one unique $-v$ for every $v$

4.1.2 Subspaces

4.8 Subspace

Let $V$ be a vector space. A nonempty set $U\subseteq V$ is called a subspace of $V$ if the following two axioms of a subspace are true for all $v,w\in U$ and all $\lambda \in \mathbb{R}$:

• $v+w\in U$ (closure addition)
• $\lambda v\in U$ (closure multiplication)

Note that the first condition is $U\subseteq V$ which must always be fulfilled!

4.9 Zero in all Subspaces

Let $U\subseteq V$ be a subspace of $V$. Then $0\in U$.

Note that this is the case since we can set $\lambda =0$ and get $0$ which has to be in all subspaces.

This means that for all subspaces, even if they’re orthogonal, $0\in U\cap V$.

4.11 Column Space is a subspace

Let $A$ be an $m\times n$ matrix. Then the column space $\text{C}(A)=\{Ax:x\in {\mathbb{R}}^n\}$ is a subspace of ${\mathbb{R}}^m$.

In the same way the rowspace and nullspace are subspaces.

4.14 Subspaces are vector spaces

Let $V$ be a vector space and $U$ a subspace of $V$. Then $U$ is also a vector space, with the same $+$ and $\cdot$.

Note that ${\mathbb{R}}^{m\times n}$ is actually not a new vector space, but instead isomorphic to ${\mathbb{R}}^{m\cdot n}$.

4.2 Bases and dimension

4.2.1 Linear combinations in vector spaces

We redefine the linear combination of a possibly infinite subset of vectors $G\subseteq V$ as a sum of the form ${\sum }_{j=1}^n{\lambda }_j{v}_j$ where $F=\{v_1,v_2,\dots ,v_n\}$ is a finite subset of $G$.

A vector space is then closed under linear combinations. Every linear combination of $V$ is again in $V$.

The set $G$ is called linearly dependent if there is an element $v\in G$ such that $v$ is a linear combination of $G\setminus \{v\}$. Otherwise, $G$ is called linearly independent. The span of $G$ written as $\text{Span}(G)$ is the set of all linear combinations of $G$.

4.2.2 Bases

4.18 Basis

Let $V$ be a vector space. A subset $B\subseteq V$ is called a basis of $V$ if $B$ is linearly independent and $\text{Span}(B)=V$.

WARNING A basis is not always a set of vectors, it is a set of elements of $U$. Thus for the subspace of diagonal matrices $D_m$, the basis is made up of diagonal matrices.

Example: The set of unit vectors $\{e_1,e_2,\dots ,e_n\}$ is the standard basis of ${\mathbb{R}}^m$.

Here the private non-zero is introduced as a non-zero entry in a vector which no other vector of the basis has. This is then used to justify that this vector is independent. Don’t use this in practice.

4.19 Basis of $A$

The set of independent columns of $A$ is a basis of the column space $\text{C}(A)$.

Basis of $\{0\}$

The basis of $\{0\}$ is $\varnothing$. Since there is no vector, $\varnothing$ is vacously independent and $\text{Span}(\varnothing )=\{0\}$ since an empty sum yields $0$.

Many bases

There are typically many bases for a vector space.

Example: Every set $B=\{v_1,v_2,\dots ,v_m\}\subseteq {\mathbb{R}}^m$ of linearly independent vectors is a basis of ${\mathbb{R}}^m$.

4.21 Finitely generated vector space

A vector space $V$ is called finitely generated if there exists a finite subset $G\subseteq V$ with $\text{Span}(G)=V$.

Example: $\mathbb{R}[x]$ is not finitely generated for example.

4.22 Existance of a Basis

Let $V$ be a finitely generated vector space and let $G\subseteq V$ be a finite subset with $\text{Span}(G)=V$. Then $V$ has a basis $B\subseteq G$.

Proof We can iteratively remove elements from $G$ that are dependent until we are left with an independent basis.

4.2.3 Steinitz exchange lemma

4.23 Steinitz exchange Lemma

Let $V$ be a finitely generated vector space, $F\subseteq V$ a finite set of linearly independent vectors (note that $F$ does not need to span $V$) and $G\subseteq V$ a finite set of vectors with $\text{Span}(G)=V$ (but they mustn’t be independent). Then the following two statements hold:

1. $|F|\le |G|$
2. There exists a subset $E\subseteq G$ of size $|G|-|F|$ such that $\text{Span}(F\cup E)=V$.

We can use the lemma to argue that there can’t be more than $n$ independent vectors in a space of dimension $n$.

4.24 All bases have the same size

Two bases $B,B^{\prime }$ of $V$ (finitely generated) satisfy $|B|=|B^{\prime }|$.

4.2.4 Dimension

4.25 Dimension

Let $V$ be a finitely generated vector space. Then $\dim (V)$ the dimension of $V$ is the size of an arbitrary basis $B$ of $V$.

4.2.5 Linear transformations between vector spaces

4.26 Linear transformation between vector spaces

Let $V,W$ be two vector spaces. A function $T:V\to W$ is called a linear transformation between vector spaces if the following linearity axiom holds for all $x_1,x_2\in V$ and all ${\lambda }_1,{\lambda }_2\in \mathbb{R}$: $T({\lambda }_1{x}_1+{\lambda }_2{x}_2)={\lambda }_{1}T(x_1)+{\lambda }_{2}T(x_2)$

4.27 Bijective linear transformations preserve bases

Let $T:V\to W$ be a bijective linear transformation between vector spaces $V$ and $W$ . Let $B=\{v1,v2,...,v_l\}\subseteq V$ be a finite set of size $l$, and let $T(B)=\{T(v_1),T(v_2),\dots ,T(v_l)\}\subseteq Q$ be the transformed set. Then $|T(B)|=|B|$. Moreover, $B$ is a basis of $V$ if and only if $T(B)$ is a basis of $W$. We therefore also have $\dim (V)=\dim (W)$.

This holds because of the bijectivity of the linear transformation.

Further, if there is one such bijective transformation, then we call the vector spaces isomorphic and $T$ an isomorphism between $V$ and $W$ (Definition 4.28). All $m$-dimensional vector spaces are isomorphic.

4.29 Basis writes each vector as unique linear combination

Let $\{v_1,\dots ,v_m\}$ be a basis of $V$. For each $v\in V$, there are unique scalars ${\lambda }_1,\dots ,{\lambda }_n$ such that $v={\sum }_{j=1}^m{\lambda }_j{v}_j$

4.2.6 Computing a vector space

4.30 Less than $\dim (V)$ vectors do not span $V$

Let $V$ be a finitely generated vector space. Let $G\subseteq V$ be a finite subset of size $|G|<\dim (V)$. Then $\text{Span}(G)\ne V$.

Using this lemma we can now state that computing a vector space means finding a basis. No smaller set of vectors can fully describe a vector space.

4.3 Computing the three fundamental subspaces

4.3.1 Column Space

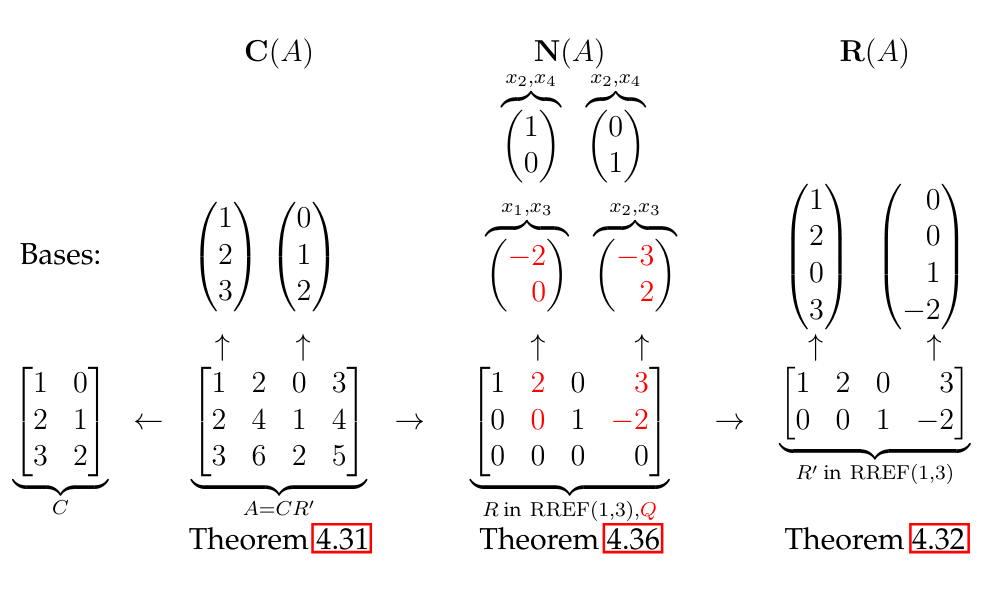
4.31 Basis of $\text{C}(A)$ from RREF

The independent columns in the RREF form of matrix $A$ are a basis of the column space and in particular: $\dim (\text{C}(A))=\text{rank}(A)=r$

It is not true that $\text{C}(A)=\text{C}(MA)$, see for example:

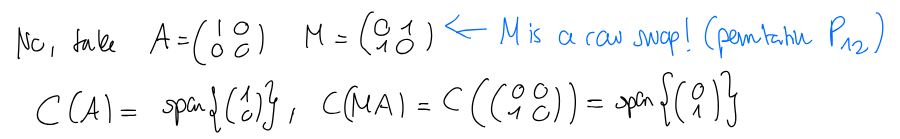
4.3.2 Row space

4.32 Basis of Row space

The first $r$ columns of $R^{\top }$ where $R$ is the RREF of $A$ form a basis of the row space (the non-zero rows). In particular $\dim (\text{R}(A))=r$

This works because as noted before, multiplying by and invertible matrix M does not change the row-space of MA on the left.

Intuitively, we are multiplying on the left by invertible matrices and thus basically take linear combinations of the rows of $A$. Thus the row-space stays the same.

Proof: $\text{R}(A)=\text{C}(A^{\top })\stackrel{!}{=}\text{C}(A^{\top }{M}^{\top })=\text{C}((MA{)}^{\top })=\text{R}(MA)$ which is true because of this:

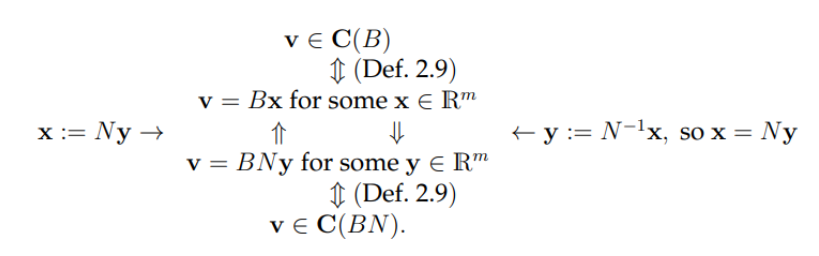
4.33 Row rank = column rank

For $A$ an $m\times n$ matrix, we have $\text{rank}(A)=\text{rank}(A^{\top })$

4.34 Rank bound

$r\le \min (n,m)$ where $r$ is the rank of $A$.

4.3.3 Nullspace

Same as with the row-space $MA$ has the same nullspace as $A$: $\text{N}(A)=\text{N}(MA)$.

How to find a basis:

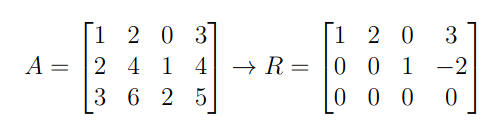
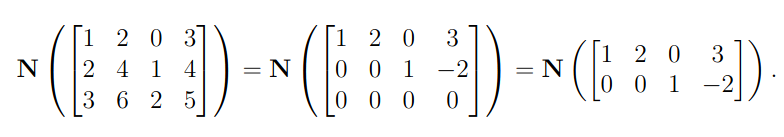Note that we can remove the zero-rows because $0^{\top }x=0$ regardless of $x$.

We now want to solve for $Rx=0$:

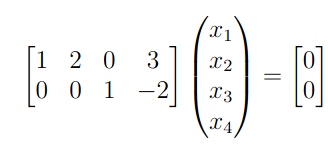
We seperate the matrix into the identity and the “rest”. Note that for this we take columns 1 and 2 as they form the 2x2 identity. 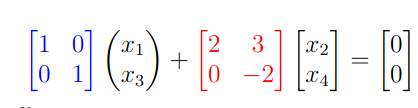Which we can transform into:

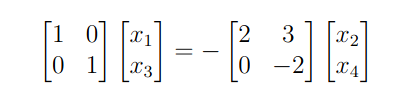
As on the left we have the identity, we reduce it to just the x vector, which gives us a system in two equations and 4 unknowns. 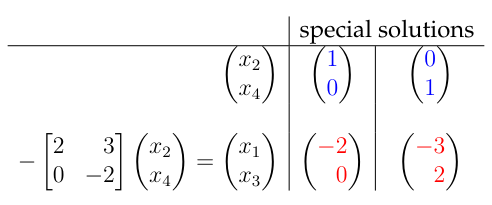We choose two special solutions (independent) and then plug in the values into our equations to find the rest. This gives us a basis of the nullspace as we get two linearly independent vectors in there and it has dimension 2. We call these particular solutions.

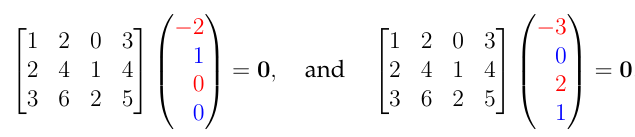
4.36 Dimension Null Space

$\dim (\text{N}(A))=n-r=n-\text{rank}(A)$

4.36 Dimension Left Null Space ( $\text{N}(A^{\top })$)

$\dim (\text{N}(A^{\top }))=m-r=m-\text{rank}(A)$

See sheet 7 where this is stated.

Summary

4.4 The solution space of $Ax=b$

4.37 Solution space of a system $Ax=b$

Let $A$ be an $m\times n$ matrix and $b\in {\mathbb{R}}^m$. The set $\text{Sol}(A,b):=\{x\in {\mathbb{R}}^n:Ax=b\}\subseteq {\mathbb{R}}^n$ is the solution space of $Ax=b$

If $b\ne 0$, $\text{Sol}(A,b)$ is unfortunately not a subspace of ${\mathbb{R}}^n$, because it doesn’t contain the zero vector! If $b\ne 0$, the the solution space is “shifted” of the origin: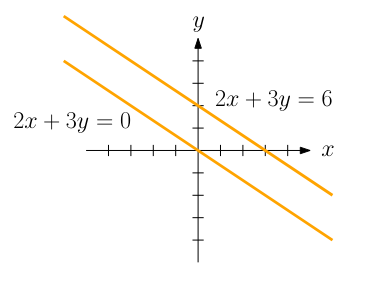

We can “fix” this by instead looking at the line through the origin. $\text{Sol}(A,0)=\text{N}(A)$ as we search for the zeros. We thus first find the nullspace, and then shift it by an arbitrary solution of $Ax=b$.

4.38 Shifting nullspace

Let $s$ be some solution of $Ax=b$. Then $\text{Sol}(A,b)=\{s+x:x\in \text{N}(A)\}$

4.4.1 Affine Subspaces

We call the solution space of $Ax=b$ an affine subspace if $b\ne 0$.

4.4.2 Number of Solutions

4.39 Dimension of solution space

If $Ax=b$ has a solution, then $\text{Sol}(A,b)$ has dimension $n-r$, where $\dim (\text{Sol}(A,b)):=\dim (\text{N}(A))$

If $A\in {\mathbb{R}}^{m\times n}$ has rank $r=m$, then $Ax=b$ has a solution for every $b\in {\mathbb{R}}^m$ (equivalent to saying that $\text{C}(A)={\mathbb{R}}^m$). We call $A$ solvable (invertible $A$ is a special case of this).

We list all possibilities:

1. If $m=n$ ($A$ is square), the system $Ax=b$ is called square. Typically solvable.
2. If $m<n$ (A is a wide matrix), the system $Ax=b$ is called underdetermined. There are typically solvable.
3. If $m>n$ (A is a tall matrix) the system $Ax=b$ is called overdetermined. Typically not solvable. (Undetermined because there are more variables that equations.)