Chapter -1.4

CR Decomposition

CR decomposition

A matrix $A\in {\mathbb{R}}^{m\times n}$ of rank $r$ can be written as the matrix-matrix product $A=C{R}^{\prime }$ where $C$ is the $m\times r$ submatrix containing the independent columns and the unique $R^{\prime }\in {\mathbb{R}}^{r\times n}$ matrix.

You can see why this works intuitively. The result of the multiplication is a matrix in $m\times n$. Each column of $R^{\prime }$ represents the number of times we take each independent column to get the dependent ones.

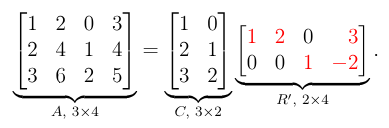
You can see that in the columns of the independent vectors, $R^{\prime }$ is such that the linear combination only contains the vector itself, once. The dependant columns are a combination of the independent ones (see column 2 being 2 times column 1, thus $R^{\prime }$ having (2, 0) as it’s second column.

Note that the C in CR’ decomposition does not need to be a column vector, it can have any width, depending on how many independent columns A has.

Invertible and Inverse Matrices

By applying the inverse matrix, you can undo any matrix transformations, as long as this matrix $A^{-1}$ exists.

If the matrix $A$ in $T_A$ is not square, the transformation is not bijective and thus not reversible.

Wide Matrix transformations are not injective

Let $T_A:{\mathbb{R}}^n\to {\mathbb{R}}^m$ be a matrix transformation and $m<n$. Then $T_A$ is not injective. This holds because a transformation from more dimensions into less loses information, so two inputs map to the same output (by the pigeonhole principle).

Tall Matrix transformations are not injective

Let $T_A:{\mathbb{R}}^n\to {\mathbb{R}}^m$ be a matrix transformation and $m>n$. Then $T_A$ is not surjective. This holds because a transformation from less dimensions into more doesn’t map to all outputs, so you can’t reverse all of them.

Now let’s look at inversible, square-matrix linear transformations.

The inverse of a bijective linear transformation is also a linear transformation

Let $T_A:{\mathbb{R}}^n\to {\mathbb{R}}^m$ be a bijective linear matrix transformation. Then $T^{-1}$ is also a linear transformation.

There are three equivalent statements about matrix transformations:

Equivalences

• (i) $T_A:{\mathbb{R}}^m\to {\mathbb{R}}^m$ is bijective.
• (ii) There is an $m\times m$ matrix B such that $BA=I$.
• (iii) The columns of $A$ are linearly independant.

The third one can be derived from the fact that if $BA=I$, there is only a single $x\in {\mathbb{R}}^m$ such that $A\text{x}=0$. It is also intuitively clear that if not all columns where linearly independent, we’d actually have a tall linear transformation and would be losing information.

Definitions and Properties of Inversible Matrices

Invertible and singular matrix

Let $A\in {\mathbb{R}}^{m\times m}$. $A$ is invertible if there is a $m\times m$ matrix $B$ such that $BA=I$ (only works if $A$ has linearly independent columns). Otherwise, $A$ is called singular.

$A$ is invertible iff (the following equivalent conditions are true):

• $AB=I$
• $BA=I$
• $AB=BA=I$

The inverse matrix is unique and can be denoted $A^{-1}$.

LEMMA

$A$, $B$ invertible matrices $m\times m$. Then $AB$ is also invertible and $(AB{)}^{-1}=B^{-1}{A}^{-1}$

LEMMA

Let $A$ be an $m\times m$ invertible matrix. Then the transpose $A^T$ is also invertible and: $$ (A^T)^{-1} = (A^-1)^T.