5. Orthogonality and Projections

5.1 Orthogonality

5.1.1 Orthogonal Subspaces

Two vectors $v,w\in {\mathbb{R}}^n$ are called orthogonal if $v^{\top }w={\sum }_{i=1}^n{v}_i{w}_i=0$. Two subspaces $V$ and $W$ are orthogonal if for all $v\in V$ and $w\in W$, the vectors $v$ and $w$ are orthogonal.

5.1.2 Subspaces Orthogonal if Basis is Orthogonal

Let $v_1,\dots ,v_k$ be a basis of subspace $V$. Let $w_1,\dots ,w_l$ be a basis of subspace $W$. $V$ and $W$ are orthogonal if and only if $v_i$ and $w_j$ are orthogonal for all $i\in \{1,\dots ,k\}$ and $j\in \{1,\dots ,l\}$.

We can determine if two subspaces are orthogonal by only comparing their basis vectors, as if they are orthogonal, all their linear combinations will also be.

As all vectors are pairwise linearly independent, their union is also linearly independent. Therefore the union of two bases is still a basis of the sum of their subspaces:

5.1.3 Basis of Subspace together form basis of ${\mathbb{R}}^n$.

Let $V$ and $W$ be orthogonal subspaces of ${\mathbb{R}}^n$. Let $v_1,\dots ,v_k$ be a basis of subspace $V$. Let $w_1,\dots ,w_l$ be a basis of subspace $W$. The set of vectors $\{v_1,\dots ,v_k,w_1,\dots ,w_l\}$ are linearly independent.

We can use this Lemma to get the basis of the subspace $V+W$, which is then indeed also a subspace of ${\mathbb{R}}^n$. This sum of orthogonal vectors is called the Minkovsky-Sum!

5.1.4 Properties of orthogonal subspaces

Let $V$ and $W$ be orthogonal subspaces. Then $V\cap W=\{0\}$ (as all subspaces contain the $0$ vector).

If $\dim (V)=k$ and $\dim (W)=l$, then $\dim (V+W)=k+l\le n$.

Note that them being orthogonal does not yet mean they are orthogonal complements. Thus their dimension is $\le$ not $=$.

5.1.5 Orthogonal Complement

Let $V$ be a subspace of ${\mathbb{R}}^n$. We define the orthogonal complement of $V$ as $V^{\perp }=\{w\in {\mathbb{R}}^n|w^{\top }v=0\text{for all }v\in V\}$

This $V^{\perp }$ is also a subspace of ${\mathbb{R}}^n$. Therefore, the concept of orthogonal subspaces allows us to decompose the space ${\mathbb{R}}^n$ into a subspace and it’s complement (these being the nullspace of $A$ and the row space of $A$).

5.1.6 Decomposition of ${\mathbb{R}}^{m\times n}$

Let $A\in {\mathbb{R}}^{m\times n}$ be a matrix. $N(A)=C(A^{\top }{)}^{\perp }=R(A)$

As we know that if $r=\dim (R(A))$ then $n-r=\dim (N(A))$. Thus they add up to the whole space!

5.1.7 Orthogonal subspace properties

Let $V,W$ be orthogonal subspaces of ${\mathbb{R}}^n$. Then the following statements are equivalent.

• $W=V^{\perp }$
• $\dim (V)+\dim (W)=n$
• Every $u\in {\mathbb{R}}^n$ can be written as $u=v+w$ with unique vectors $v\in V$, $w\in W$

In words, this means that we can combine two orthogonal subspaces and create a new subspace, whose dimension is the sum of the two dimensions.

Example We can write: ${\mathbb{R}}^n=V+V^{\perp }=\{v+w\mid v\in V,w\in V^{\perp }\}$(this is a Minkovsky sum). We can also write ${\mathbb{R}}^n=V^{\perp }+(V^{\perp }{)}^{\perp }$, it’s symmetric.

5.1.8 Orthogonality cancels out

Let $V$ be a subspace of ${\mathbb{R}}^n$. Then $V=(V^{\perp }{)}^{\perp }$

This allows us to rewrite Theorem 5.1.6:

5.1.9 Four fundamental Subspaces

Let $A\in {\mathbb{R}}^{m\times n}$. $N(A)=C(A^{\top }{)}^{\perp }\text{and}C(A^{\top })=N(A{)}^{\perp }$

Subspace Orthogonality

We have: $N(A{)}^{\perp }=C(A^{\top })$ and $N(A^{\top })=C(A{)}^{\perp }$

We can visualise the four fundamental subspaces in the following way:

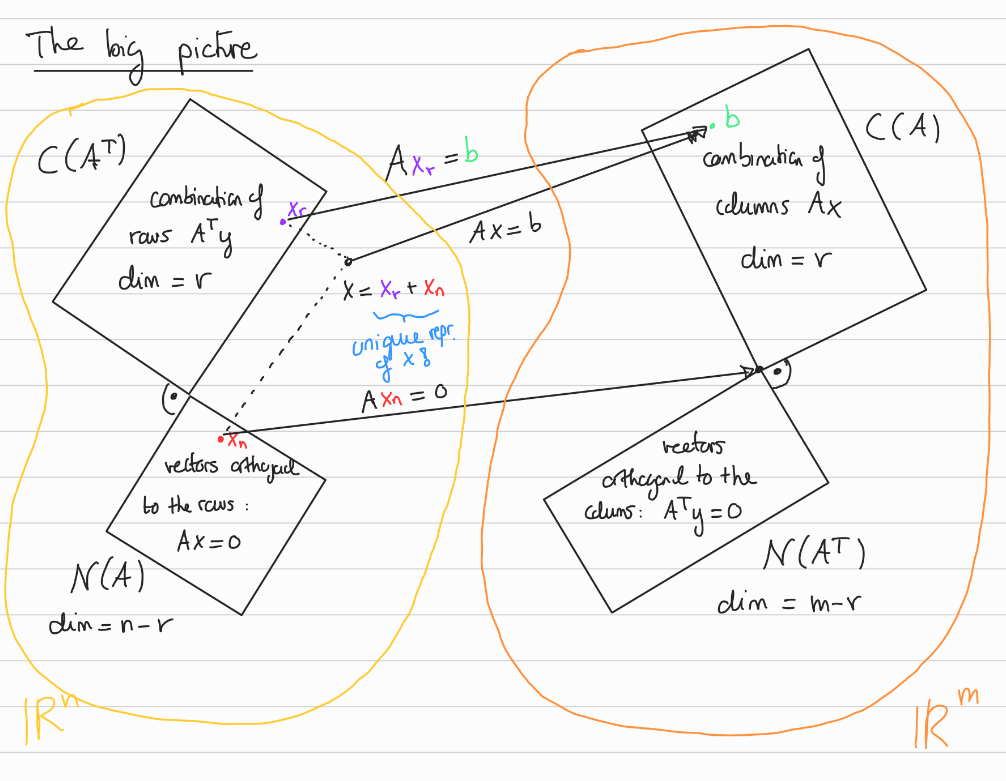
Consequences: Recall that the complete solution to $Ax=b$ (“all $x$‘s st $Ax=b$“) $\text{Sol}(A,b)=\{x\in {\mathbb{R}}^n\mid x=x_p+x_n,x_n\in N(A)\}=x_p+N(A)=\text{"one }{x}_p\text{ + any }{x}_n\text{"}$ where $x_p$ is a particular solution (assuming the system is feasible).

You can show that $\text{Sol}(A,b)$ is also equal to $x_r+N(A)=\text{"}{x}_r\text{ + any }{x}_n\text{"}$, where $x_r\in C(A^T)=R(A)$ and $x_n\in N(A)$ and where $x_r\in C(A^T)$ is unique (i.e. such a particular solution $x_p=x_r\in R(A)$ always exists and is unique) (See Sabatino Notes Week 9 for Proof.)

5.1.10 $A$ and $A^{\top }A$

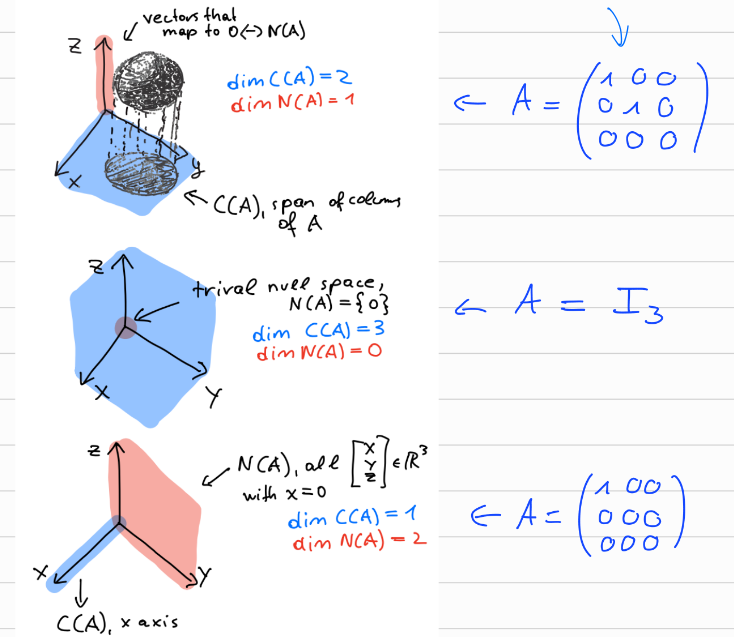
Let $A\in {\mathbb{R}}^{m\times n}$. Then $N(A)=N(A^{\top }A)$ and $C(A^{\top })=C(A^{\top }A)$.

Why is this needed?

• $N(A)=N(A^{\top }A)$: if $N(A)=\{0\}$ i.e. $A$ lin. indep. columns then $N(A^{\top }A)$ invertible as $N(A^{\top }A)=\{0\}$ and square.
• $C(A^{\top })=C(A^{\top }A)$: needed so $A^{\top }A\hat{x}$ is in the same subspace as $A^{\top }b$.

This one is important! Learn the proof! $N(A)=N(A^{\top }A)$ holds because:

• if $x\in N(A)$ then $Ax=0⟹A^{\top }Ax=A\cdot 0⟹A^{\top }Ax=0$.
• if $x\in N(A^{\top }A)$ then $A^{\top }Ax=0$, which means $0=x^{\top }0=x^{\top }{A}^{\top }Ax=(Ax{)}^{\top }(Ax)=||Ax|{|}^2⟹Ax=0$ $C(A^{\top })=C(A^{\top }A)$ holds because:
• if $x\in C(A^{\top }A)$ then let $\exists y{A}^{\top }Ay=x$ and if we set $z=Ay$ then $A^{\top }z=x$ thus $x\in C(A^{\top })$.
• $C(A^{\top })=N(A{)}^{\perp }=N(A^{\top }A{)}^{\perp }$ as ($N(A^{\top }A)=N(A)$). Then $N(A^{\top }A{)}^{\perp }=C((A^{\top }A{)}^{\top })$ (by $N(B{)}^{\perp }=C(B^{\top })$) and $(A^{\top }A{)}^{\top }=A^{\top }A$ thus $C(A^{\top })=C(A^{\top }A)$.

5.2 Projections

If a system $Ax=b$ has no solutions (because $A$ is not invertible, i.e. $b\notin C(A)$) can we find a $p\in C(A)$ such that the error is minimal - basically the next best solution?

This usually happens when we have more equations than variables (i.e. each is being “overdetermined”) $m\ge n$ (alternative phrasing: there aren’t enough vectors to span the space, thus $C(A)$ is a line or a plane in 3d for example).

5.2.1 Projection of a vector onto a subspace

The projection of a vector $b\in {\mathbb{R}}^m$ onto a subspace $S$ (of ${\mathbb{R}}^m$) is the point in $S$ that is closest to $b$. In other words ${\text{proj}}_S(b)={\text{argmin}}_{p\in S}||b-p||$

Where $b=p+e⟹b-p=e$, with $e$ the error.

The one-dimensional case

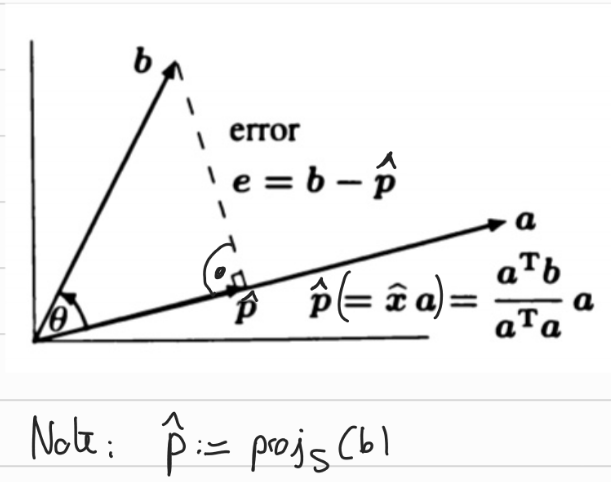
We can clearly see that the error vector in 2d is orthogonal to the projection $e^{\top }a=(b-p{)}^{\top }a$ by geometric intuition.

5.2.2 Projection in 2d formula

Let $a\in {\mathbb{R}}^m\backslash \{0\}$. The projection of $b\in {\mathbb{R}}^m$ on $S=\{\lambda a|\lambda \in \mathbb{R}\}=C(a)$ is given by ${\text{proj}}_S(b)=\frac{a{a}^{\top }}{a^{\top }a}b$ This minimiser is unique.

And indeed if we substitute we find that the error vector is indeed orthogonal to $a$.

Intuition: (In the lecture we don’t assume orthogonality of the error vector).

• Assume $\mathbf{a}\perp \mathbf{e}$ $⟹$ $\mathbf{a}\perp (\mathbf{b}-\mathbf{p})$ (define error vector $\mathbf{e}=\mathbf{b}-\mathbf{p}$).
• We can write $\mathbf{p}=\lambda \mathbf{a},\lambda \in \mathbb{R}$ since we know the projection vector is on the line spanned by $\mathbf{a}$ and hence $\mathbf{p}$ is a scalar multiple of $\mathbf{a}$. \begin{align} \mathbf{a} \perp (\mathbf{b} - \mathbf{p}) &\iff \mathbf{a}^\top(\mathbf{b} - \mathbf{p}) = 0 \\ &\iff \mathbf{a}^\top(\mathbf{b} - \lambda\mathbf{a}) = 0 \\ &\iff \mathbf{a}^\top\mathbf{b} - \mathbf{a}^\top\lambda\mathbf{a} = 0 \\ &\iff \mathbf{a}^\top\mathbf{b} = \mathbf{a}^\top\lambda\mathbf{a} \\ &\iff \mathbf{a}^\top\mathbf{b} = \lambda\mathbf{a}^\top\mathbf{a} \\ &\iff \lambda = \frac{\mathbf{a}^\top\mathbf{b}}{\mathbf{a}^\top\mathbf{a}} \end{align}
• Where we first used $\mathbf{v}\perp \mathbf{u}⟺{\mathbf{v}}^{\top }\mathbf{u}=0$, then plugged in $\lambda \mathbf{a}$ for $\mathbf{p}$, then used the distributivity of the vector multiplication.
• We can divide by ${\mathbf{a}}^{\top }\mathbf{a}$ (${\mathbf{a}}^{\top }\mathbf{a}$ is a nonzero real number, as $\mathbf{a}$ is a nonzero vector)

We can then plug in $\lambda$ into $p=\lambda \mathbf{a}$ to get the projection vector $\mathbf{p}=\frac{a^{\top }b}{a^{\top }a}a=\frac{a{a}^{\top }}{a^{\top }a}b$We can do this since $a^{\top }b$ is a scalar so $(a^{\top }b)a=a(a^{\top }b)=(a{a}^{\top })b$ (commute and associativity).

Idempotence in 1d: if we want to find the projection of a vector $b=\lambda a$, then the projection simply returns $\lambda a$, as $b$ is already on the line (subspace).

General Case

5.2.3 Projection is well defined

The projection of a vector $b\in {\mathbb{R}}^m$ to the subspace $S=C(A)$ is well defined. It can be written as ${\text{proj}}_S(b)=A\hat{x}$ where $\hat{x}$ satisfies the normal equations $A^{\top }A\hat{x}=A^{\top }b$

Intuition:

• In the previous case, we had $\mathbf{e}=(\mathbf{b}-pro{j}_S(\mathbf{b}))\perp \mathbf{a}$. Here, the same orthogonality condition holds for all columns of $A$ (that we are projecting on).
• This is the same as stating $A^{\top }(\mathbf{b}-pro{j}_S(\mathbf{b}))=0$ which by substituting $pro{j}_S(b)=\mathbf{p}=A\hat{\mathbf{x}}$ gives $A^{\top }\mathbf{b}-A^{\top }A\hat{\mathbf{x}}=0$ which we can restate as $A^{\top }A\hat{\mathbf{x}}=A^{\top }\mathbf{b}$, which is the normal equation.

Unique solution

If $A^{T}A$ is invertible, we have a unique solution $\hat{x}$ that satisfies the equation: $p=A\hat{x}=A(A^{\top }A{)}^{-1}{A}^{\top }b$

From $A^{\top }A\hat{\mathbf{x}}=A^{\top }\mathbf{b}$ we can construct a formula for $\mathbf{p}$: $(A^{\top }A{)}^{-1}(A^{\top }A)\hat{\mathbf{x}}=(A^{\top }A{)}^{-1}{A}^{\top }\mathbf{b}$ ($A^{\top }A$ invertible if the columns of $A$ are independent), which gives us $A\hat{\mathbf{x}}=A(A^{\top }A{)}^{-1}{A}^{\top }\mathbf{b}=\mathbf{p}$.

5.2.4 $A^{\top }A$ invertible $\iff$ $A$ has indep. columns

$A^{\top }A$ is invertible if and only if $A$ has linearly independent columns.

5.2.5 Projection Matrix

Let $S$ be a subspace in ${\mathbb{R}}^m$ and $A$ a matrix whose columns are a basis of $S$. The projection of $b\in {\mathbb{R}}^m$ to $S$ is given by ${\text{proj}}_S(b)=Pb$ where $P=A(A^{\top }A{)}^{-1}{A}^{\top }$ is the projection matrix.

Note the condition for the columns to be a basis - this forces them to be independent, which means $A^{\top }A$ invertible by Lemma 5.2.4.

IMPORTANT It may look like we can simplify the expression for the projection matrix $P$. This is not the case as $(A\top A{)}^{-1}=A^{-1}(A^{\top }{)}^{-1}$ is only the case if $A$ itself is invertible. But if $A$ is invertible, it spans ${\mathbb{R}}^m$ anyways and any projection is simply the point itself. This is beautifully reflected in the fact that if we simplify $P=A{A}^{-1}(A^{\top }{)}^{-1}{A}^{\top }$ then we simply get $P=I$.

5.2.6

If $b\in {\mathbb{R}}^m$ then ${\text{proj}}_S({\text{proj}}_S(b))={\text{proj}}_S(b)$ by definition. This requires us to have that $PPb=Pb\iff P^2=P$.

We also say $P$ is idempotent.

$P$ is symmetric (reprove in exam)

For $P$ we have that $P^{\top }=P$.

Proof: $P^{\top }=(A(A^{\top }A{)}^{-1}{A}^{\top }{)}^{\top }=$ $(A^{\top }{)}^{\top }{(A^{\top }A{)}^{-1}}^{\top }{A}^{\top }=A(A^{\top }A{)}^{-1}{A}^{\top }=P$ We use the fact that for invertible matrices ${M^{-1}}^{\top }={M^{\top }}^{-1}$.

5.2.6

Let $S^{\perp }$ be the orthogonal complement of $S$ and $P$ the projection matrix onto $S$ Then $I-P$ is the projection matrix that maps $b\in {\mathbb{R}}^m$ to ${\text{proj}}_{S^{\perp }}(b)$.

Proof Idea: Since $b=e+{\text{proj}}_S(b)=e+Pb$ with $e\in S^{\perp }$ Thus $(I-P)b=b-Pb=e={\text{proj}}_{S^{\perp }}(b)$This is true, since it holds that indeed $I-P$ is also idempotent: $(I-P{)}^2=I-2P+P^2=I-P-P+P=I-P$