Chapter 6

6.1 Least Squares Approximation

One case in which $Ax=b$ usually has no solutions is when trying to fit a line to a set of measurements or datapoints. We can then try to use a least squares approximation to find a best-fitting line.

6.1.1 Minimiser is solution to the normal equations

A minimiser of ${\min }_{\hat{x}\in {\mathbb{R}}^n}||A\hat{x}-b|{|}^2$ is also a solution of $A^{\top }A\hat{x}=A^{\top }b$. When $A$ has independent columns the unique minimiser of $\hat{x}$ is given by $\hat{x}=(A^{\top }A{)}^{-1}{A}^{\top }b$

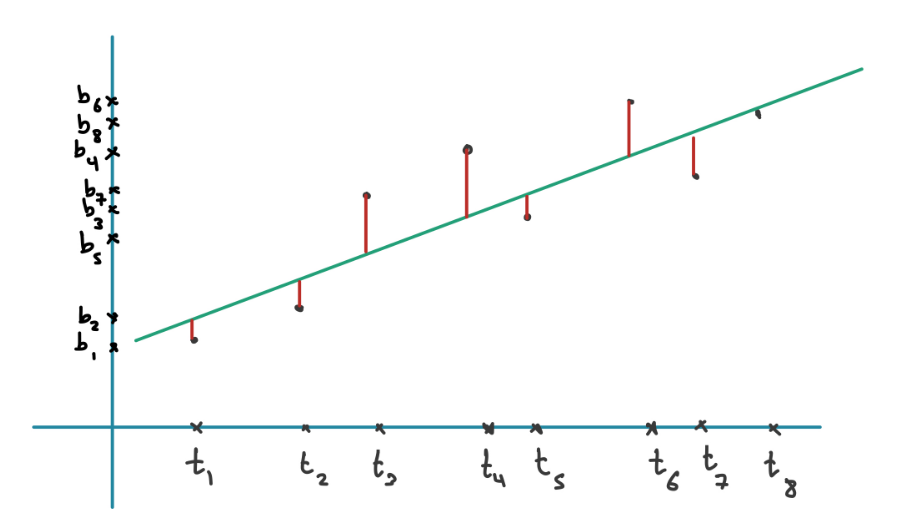
The line here can be represented by the equation $f(x)={\alpha }_{1}x+{\alpha }_0$. We want to find ${\alpha }_0$ and ${\alpha }_1$ that minimise the sum of squares of the error of the fitted line: ${\min }_{{\alpha }_0,{\alpha }_1}{\sum }_{k=1}^m(b_k-[{\alpha }_0+{\alpha }_1{t}_k]{)}^2$ which in Matrix vector notation gives ${\min }_{{\alpha }_0,{\alpha }_1}||b-A\left(\begin{array}{c}{\alpha }_1\\ {\alpha }_0\end{array}\right)|{|}^2$ where $b=\left(\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_m\end{array}\right)$ and $A=\left[\begin{array}{cc}1& t_1\\ 1& t_2\\ ⋮& ⋮\\ 1& t_{m-1}\\ 1& t_m\end{array}\right]$

6.1.2 Independent columns of $A$

The columns of the $m\times 2$ matrix defined before are linearly dependent if and only if $t_i=t_j$ for all $i\ne j$.

As all datapoints are unique in time (can’t have two points at one time) this always holds.

6.1.3

If the columns of $A$ are pairwise orthogonal, we get $A^{\top }A$ a diagonal matrix which is very easy to invert. We can convert any $A$ to have orthogonal columns by making sure that the sum of all the $t_k=0$, which can be achieved by shifting the graph on the x-axis.

We can also try to fit any other equation, not just a line here. A parabola could be used by adding a third column to $A$ which contains $t^2$ and adding ${\alpha }_2$.

6.2 The set of all solutions to a system of linear equations

We know that $\forall x\in {\mathbb{R}}^n$, there exist $x_0\in N(A)$ and $x_1\in R(A)$ such that $x=x_0+x_1$ and $x_1^{\top }{x}_0=0$ as $N(A)=C(A^{\top }{)}^{\perp }$ are orthogonal complements.

6.2.1 Unique solutions

Let $A\in {\mathbb{R}}^{m\times n}$. Let $x,y\in C(A^{\top })$. We have that $Ax=Ay\iff x=y$

Proof This is because $x,y$ have unique decompositions into the two fundamental subspaces. $Ax=Ay\iff x-y\in N(A)\iff x^{\top }(x-y)=0=y^{\top }(x-y)\iff (x-y{)}^{\top }(x-y)=0$ and from this follows that $||x-y|{|}^2=0⟹x-y=0$.

6.2.2 Unique solution to a system

Suppose that $\{x\in {\mathbb{R}}^n|Ax=b\}\ne \varnothing$. Then $\{x\in {\mathbb{R}}^n|Ax=b\}=x_1+N(A)$ where $x_1\in R(A)$ is unique such that $A{x}_1=b$.

This means that if there’s more than one solution to the system (i.e. the nullspace is not $=\{0\}$), then the set of all solutions is a specific solution + the entire nullspace.

6.2.3 Unique in $C(A^{\top }A)$

Suppose that $\{x\in {\mathbb{R}}^n|Ax=b\}\ne \varnothing$. Then there exists a unique vector $x_1\in C(A^{\top }A)$ such that $A{x}_1=b$

The empty solution

We now only need to analyse the case where the given system of linear equations has no solutions: $\{x\in {\mathbb{R}}^n|Ax=b\}=\varnothing$.

This is difficult as proving a negative in this case means exhausting the entire search space (which is infinite) or proving it by using something smarter.

We can issue a “certificate” which proves that a system has no solution.

6.2.4 Proving no solutions

$\{x\in {\mathbb{R}}^n|Ax=b\}=\varnothing ⟺\{z\in {\mathbb{R}}^m|A^{\top }z=0,b^{\top }z=1\}\ne \varnothing$

Proof:

• Verify that $P\ne \varnothing \wedge D\ne \varnothing$ is impossible:
  • If $x\in P$ and $z\in D$ then $0=0^{\top }x=z^{\top }Ax=z^{\top }b=1$
• We now want to show that if $P=\varnothing ⟹D\ne \varnothing$:
  • $P=\varnothing ⟹b\notin C(A)$ (there are no solutions) $⟺b-{\text{proj}}_{C(A)}(b)\ne 0$ (there is an error, $e=b-{\text{proj}}_{C(A)}\in N(A^{\top })$
    • Thus $e\ne 0$ and $z:=\frac{1}{e^{\top }e}e$
    • $z\in N(A^{\top })⟹A^{\top }z=0$
    • $b^{\top }z=\frac{1}{e^{\top }e}{e}^{\top }b=\frac{1}{e^{\top }e}{b}^{\top }e$ but we can rewrite $b=(p+e)$ and thus $b^{\top }z=\frac{1}{e^{\top }e}{p}^{\top }e+\frac{1}{e^{\top }e}{e}^{\top }e$
      • we know the first term is $0$ as $p^{\top }e=0$ as they are in orthogonal subspaces
      • the second term is $1$ as it’s $\frac{e^{\top }e}{e^{\top }e}$.
  • Thus $z\in D$

Example:

• $P=\{x\in {\mathbb{R}}^3|x_1+2x_2-x_3=1,2x_1+4x_2-2x_3=0\}$
• The system $D=\{z\in {\mathbb{R}}^m|A^{\top }z=0,b^{\top }z=1\}$ is then $$ D = { z \in \mathbb{R}^2 \ | \ z_1 + 2z_2 = 0, 2z_1 + 4z_2 = 0, -z_1 - 2z_2 = 0, z_1 = 1 } $$$P = \emptyset$and$D \neq \emptyset$because$z = (1, -\frac{1}{2})^\top \in D$.

Applications:

1. If our matrix $A\in {\mathbb{R}}^{m\times n}$ had linearly independent rows, then there would be solutions for all points in $b\in {\mathbb{R}}^m$. Since the rows are linearly independent, the only solution to $z^{\top }A=0$ is $z=0$. Hence $z^{\top }b=0\ne 1$. Thus there is always a solution for the $P$.
2. We can also show that a vector $b$ is linearly independent from a set of vectors $a_1,\dots ,a_n$. We just put them into the matrix equation $Ax=b$. If there is no solution, $b$ is independent. But to show the system has no solutions, we need our new formula.